Sawtooth pattern needs tuneup

[thumbnail at .5 sub-pixel zoom -- click on image to expand]

attempted sawtooth pattern with incorrect timing --
runs for three cycles and then blows up.
The generations where the line burns out to
create a block are 3648, 9952, 20896, and 39800.
Their remainders modulo 192 are 0, 160, 160, and 56.
The growth in the generation numbers is
approximately a factor of 1.72.

David Bell, 18 July 2005

Adapted from notes by David Bell:

For the sawtooth to be made functional, the remainders of the generation numbers where the line burns out (modulo 192) must either be constant or else oscillate only over a few "safe" values.

The sawtooth can be easily modified by shifting the glider reflectors forwards or backwards along the path and by adjusting when the beehive is turned into the backward glider. But simply bouncing the gliders back using the glider reflectors might not be good enough; it might be necessary to hold onto them until the right generation numbers before releasing them.

Alternative sawtooth mechanism

David Bell, 18 July 2005

Another sawtooth mechanism: a pair of gliders can arrive from the end of the line to cleanly ignite it while sending a glider back to the source direction. Perhaps the timings involved in this alternative mechanism would be easier:

Update: 16 August 2005

another attempted sawtooth with incorrect timing --
runs for about 342,000 ticks and then blows up.
A p1056 gun is attached to a p8 regulator
in place of the original simple reflectors.
Dave Greene, 16 August 2005

Notes by Dave Greene:
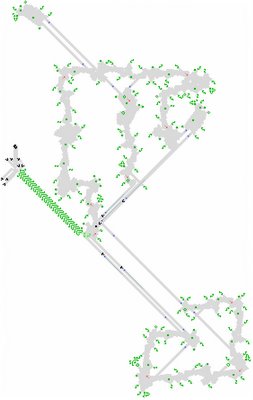
I tried replacing the reflectors at the stationary end of the pattern with a p8 universal regulator, and ended up with an almost-sawtooth that works nicely for 342,000 generations -- and then blows up. Apparently my math is still wrong somewhere...

My one useful result was that a line-igniting glider can be delayed by any multiple of 176 generations, and the burning fuse will still arrive at the active site at the same phase of the p192 lineship. [After 192 generations the fuse is longer by 16 cells, so it takes 16 ticks longer to burn. So to keep the burning fuse from arriving late at the active site, you have to subtract 16 ticks from 192].

-- So I attached a p1056 gun (6 x 176) to the universal regulator, and found a configuration that survives for quite a few cycles... apparently by sheer luck, since there's something wrong with the underlying theory. The problem seems to be that the ever-increasing return time of the glider also extends the length of the fuse by a variable amount -- and the fuse burns four times as fast as a glider travels, so it's easy for the feedback effect to result in several possible arrival times. The burning-out reaction is versatile enough to handle any amount of lateness up to 80 ticks or so after the phase used for the first couple of cycles -- but eventually a phase always seems to come along that is off by more than that.

I also tried p880 and p2112 drive guns [I thought I had accounted for the variable fuse lengths with p2112, which is LCM(176,192) -- but no such luck.] It seems possible that delaying one of these drive guns by some number of generations would get the pattern into a stable cycle -- I just haven't figured out how to predict this in advance yet, and brute-force searching is fairly tedious in this case. Anyway, it wouldn't be quite as interesting to get the right answer by accident!

I tried writing equations to predict the length of later cycles, given the glider travel time and fuse burning time and the phase of the burning fuse's arrival at the active site... but so far I've always ended up with wrong answers after a cycle or two. Haven't given up yet, but would be happy if someone else wanted to figure it out!

Perpendicular greyship update

Update: 22 July 2005 07:22

Hartmut Holzwart has produced some new partial results related to perpendicular greyships -- i.e., spaceships whose central section is made up of alternating lines of ON and OFF cells, and whose direction of travel is perpendicular to these lines. Several completed spaceships of this type are shown in an upcoming weblog posting.

Connection of 1/10 slope to 1/2 slope
Hartmut Holzwart, 14 July 2005

A 1/10-slope edge can be connected to a 1/2-slope edge:

Connection from side of perpendicular 
greyship to 1/4-slope back edge

Hartmut Holzwart, 22 July 2005

Jason Summers' side component can be connected to the 1/4 back edge component; however, Holzwart reports that his attempts to connect the side component to a known front component have not been successful.

Greyship details

Jul 1:

#C diamond-shaped greyship  Hartmut Holzwart  1 Jul 2005
x = 88, y = 83, rule = B3/S23
50bobo$49bobbo$48boo$47bo3bo$46b3obo$45bo$44b7o$5bobo35bo9boboo$4bobbo
34b12ob3o$3boo36bo16bo$bbo37b17obbo$b4o34bo19boo$o4bo32b23o$obbo33bo
21bo$obbo32b23o$bo33bo25boboo$bb4obo26b28ob3o$3bo3bo25bo32bo$4bo27b33o
bbo$4bobo24bo35boo$30b39o$3b3o23bo37bo$3boo23b39o$3b3o21bo41boboo$26b
44ob3o$4bobo18bo48bo$4bo19b49obbo$3bo3bo15bo51boo$bb4obo14b55o$bo19bo
53bo$obbo16b55o$obbo15bo57boboo$o4bo12b60ob3o$b4o12bo64bo$bbo13b65obbo
$3boo10bo67boo$4bobbobo4b71o$5bobobbobbo69bo$8bo3b71o$9bo75bobo$10b76o
bo$$10b76obo$9bo75bobo$8bo3b71o$5bobobbobbo69bo$4bobbobo4b71o$3boo10bo
67boo$bbo13b65obbo$b4o12bo64bo$o4bo12b60ob3o$obbo15bo57boboo$obbo16b
55o$bo19bo53bo$bb4obo14b55o$3bo3bo15bo51boo$4bo19b49obbo$4bobo18bo48bo
$26b44ob3o$3b3o21bo41boboo$3boo23b39o$3b3o23bo37bo$30b39o$4bobo24bo35b
oo$4bo27b33obbo$3bo3bo25bo32bo$bb4obo26b28ob3o$bo33bo25boboo$obbo32b
23o$obbo33bo21bo$o4bo32b23o$b4o34bo19boo$bbo37b17obbo$3boo36bo16bo$4bo
bbo34b12ob3o$5bobo35bo9boboo$44b7o$45bo$46b3obo$47bo3bo$48boo$49bobbo$
50bobo!

July 2:

#C front and sides for square greyship  Jason Summers 2 Jul 2005
x = 46, y = 63, rule = B3/S23
10bo$$10bo$$10bo4$8bo3bo$8bo3b27o$9bo$10b29o$$10b29o$9bo$8bo3b27o$8bo
3bo$8bo3b27o$9bo$10b29o$$10b29o$9bo$8bo3b27o$8bo3bo$8bo3b27o$9bo$10b
29o$$10b29o$9bo$8bo3b5obobb5obobob5obo$5bobobbobbo4bobobo3boobobbo4bo$
4bobbobo4boo8boo3bo3boo6bobobo$3boo10bobbo5b4o6bobbo$bbo13bobo8bobo5bo
bo$b4o15bo8bo$o4bo14bo8boo$obbo16boobo6b3o$obbo19bo8bo$bo$bb4obo$3bo3b
o$4bo$4bobo$$3b3o$3boo$3b3o$$4bobo$4bo$3bo3bo$bb4obo$bo$obbo$obbo$o4bo
$b4o$bbo$3boo$4bobbo$5bobo!

July 4:

#C 2c/4 45-90-45 triangle greyship  Hartmut Holzwart  4 Jul 2005
x = 100, y = 59, rule = S23/B3
48bobo$47bobbo$46boo$45bo3bo$44b3obo$7bo35bo$4b4o35b6o$4boo35bo9boboo$
bbo38b11ob3o$bb4o33bo16bo$bo37b16obbo$3obbo31bo19boo$b3o33b22o$bbo32bo
21bo$3b3obo27b22o$3bobboo25bo25boboo$4b3o26b27ob3o$6bo24bo32bo$4bo26b
32obbo$4bobo22bo35boo$3bo25b38o$4bobo20bo37bo$4bo22b38o$6bo18bo41boboo
$4b3o18b43ob3o$3bobboo15bo48bo$3b3obo15b48obbo$bbo18bo51boo$b3o17b54o$
3obbo13bo53bo$bo17b54o$bb4o11bo57boboo$bbo14b59ob3o$4boo9bo64bo$4b4obo
5b64obbo$7boobobbo67boo$9boobb70o$10boo69bo$11b70o10b3o3bo$83booboobb
7obbo$9b75o10bobboo$8boo78b3o6boo$7boobb3obb4obb4obb4obb4obb4obb4obb4o
bb4obb4obb4obb4obboobbobbo$6b3obb3obobboobobboobobboobobboobobboobobb
oobobboobobboobobboobobboobobboobobboo$7bobo7bo5bo5bo5bo5bo5bo5bo5bo5b
o5bo5bo5bo7b4o$8b3o80bo3bo$7bobboo79bo$10b3obbo76bobbo$10b3obbo$4boo7b
o$3boob5oboo$4b6ob3obo$5b3o3bobb3oboboo$13booboboo$11bo9boo$9boobbob3o
bobboboo$9bo4bobbobobooboo$9bo3boo5b3obo$10b3o7boo!

#C 45-90-45-triangle greyship with p2 technology except on backslope
#C Hartmut Holzwart  4 Jul 2005
x = 85, y = 74, rule = B3/S23
48bobo$47bobbo$46boo$45bo3bo$44b3obo$7bo35bo$4b4o35b6o$4boo35bo9boboo$
bbo38b11ob3o$bb4o33bo16bo$bo37b16obbo$3obbo31bo19boo$b3o33b22o$bbo32bo
21bo$3b3obo27b22o$3bobboo25bo25boboo$4b3o26b27ob3o$6bo24bo32bo$4bo26b
32obbo$4bobo22bo35boo$3bo25b38o$4bobo20bo37bo$4bo22b38o$6bo18bo41boboo
$4b3o18b43ob3o$3bobboo15bo48bo$3b3obo15b48obbo$bbo18bo51boo$b3o17b54o$
3obbo13bo53bo$bo17b54o$bb4o11bo57boboo$bbo14b59ob3o$4boo9bo64bo$4b4obo
5b64obbo$7boobobbo67boo$9boobb70o$10boo69bo$11b70o$$13b70obo$12boo69b
oo$11boobb4obobob5obobb5obobob5obobb5obobob5obobb5obobob3o$9boobobbo3b
oobobbo4bobobo3boobobbo4bobobo3boobobbo4bobobo3boobobboo$6b4obo5boo3bo
3boo8boo3bo3boo8boo3bo3boo8boo3bo$6boo9b4o6bobbo5b4o6bobbo5b4o6bobbo5b
4o$4bo15bobo5bobo8bobo5bobo8bobo5bobo8bobo$4b4o14bo9bo8bo9bo8bo9bo8bo$
3bo18boo8bo8boo8bo8boo8bo8boo$bb3obbo15b3o6boobo6b3o6boobo6b3o6boobo6b
3o$3b3o19bo9bo8bo9bo8bo9bo8bo$4bo$5b3obo$5bobboo$6b3o$8bo$6bo$6bobo$5b
o$6bobo$6bo$8bo$6b3o$5bobboo$5b3obo$4bo$3b3o$bb3obbo$3bo$4b4o$4bo$6boo
$6b4o$9bo!

#C greyship w/ back at limit slope ~1/4  Hartmut Holzwart  4 Jul 2005
x = 95, y = 120, rule = B3/S23
50bobo$49bobbo$48boo$47bo4bo$46b4obbo$45bo$45b3obobboo$7bo35bo6bobo$4b
4o35b8obbo$4boo35bo10bobo$bbo38b11obbo$bb4o33bo14boboo$bo37b14obobo$3o
bbo31bo16bobo$b3o33b18obo$bbo32bo18boboboo$3b3obo27b19obbo$3bobboo25bo
20boboboo$4b3o26b21obbobo$6bo24bo24boboo$4bo26b24obobo$4bobo22bo26bobo
$3bo25b28obo$4bobo20bo28boboboo$4bo22b29obbo$6bo18bo30boboboo$4b3o18b
31obbobo$3bobboo15bo34boboo$3b3obo15b34obobo$bbo18bo36bobo$b3o17b38obo
$3obbo13bo38boboboo$bo17b39obbo$bb4o11bo40boboboo$bbo14b41obbobo$4boo
9bo44boboo$4b4obo5b44obobo$7boobobbo46bobo$9boobb48obo$10boo48boboboo$
11b49obbo$60boboboo$11b49obbobo$10boo50boboo$9boobb48obobo$7boobobbo
48bobo$4b4obo5b48obo$4boo9bo46boboboo$bbo14b45obbo$bb4o11bo44boboboo$b
o17b43obbobo$3obbo13bo44boboo$b3o17b42obobo$bbo18bo42bobo$3b3obo15b42o
bo$3bobboo15bo40boboboo$4b3o18b39obbo$6bo18bo38boboboo$4bo22b37obbobo$
4bobo20bo38boboo$3bo25b36obobo$4bobo22bo36bobo$4bo26b36obo$6bo24bo34bo
boboo$4b3o26b33obbo$3bobboo25bo32boboboo$3b3obo27b31obbobo$bbo32bo32bo
boo$b3o33b30obobo$3obbo31bo30bobo$bo37b30obo$bb4o33bo28boboboo$bbo38b
27obbo$4boo35bo26boboboo$4b4o35b25obbobo$7bo35bo26boboo$45b24obobo$45b
o24bobo$47b24obo$47bo22boboboo$49b21obbo$49bo20boboboo$51b19obbobo$51b
o20boboo$53b18obobo$53bo18bobo$55b18obo$55bo16boboboo$57b15obbo$57bo
14boboboo$59b13obbobo$59bo14boboo$61b12obobo$61bo12bobo$63b12obo$63bo
10boboboo$65b9obbo$65bo8boboboo$67b7obbobo$67bo8boboo$69b6obobo$69bo6b
obo$71b6obo$71bo4bobobobo$73b3obbo3bo$73bobbo5boo$75bo4boob3obbo$74bo
3bobo3b3obo$74b3o6bobo$72boobo6boobo$71boboboo4boobooboobobo$71bobb3o
5bo4bo$71booboo7b4o3bobbo$73boo10bo4boobo$$91boo$89bo4bo$88bo$88bo5bo$
88b6o!

Jul 5:

#C junctions to construct arbitrary greyship front-edge slopes, 0-90
#C Jason Summers  5 Jul 2005
x = 95, y = 66, rule = B3/S23
9bobo17b30o$8bobbo18bo$7boo22b28o$6bo3bo21bo$5b3obo23b26o$bboo30bo$bo
3b5o25b24o$o3bo31bo$o5boo29b22o$3o3b4o28bo$bo7bo29b20o$boo37bo$bobo23b
obo4bobo4b18o$boobboobo8bobo6bobboboobobbo4bo$bbob3obo3bob4obobo3boo8b
o7b16o$9booboboobbobbobbo4bo6bobboobbo$4b6oboo3b4obob5obo7b4obboobb12o
$5bo4b3o6bo11boo10boobo$6boo5boobboobbob5obo7b4obboobb12o$7bobbo5b4obo
bbo4bo6bobboobbo$8boboboo5bobo3boo8bo7b16o$26bobboboobobbo4bo$27bobo4b
obo4b18o$40bo$39b20o$38bo$37b22o$36bo$35b24o$34bo$33b26o$32bo$31b28o$
30bo$29b30o$26boo$25bo3b30o$24bo3bo$24bo5b29o$24b3o3bo$25bobo4b63o$25b
oobbobbo$23bo3boo4b62o$22boo10bo$23b6o6b60o$24bo4bo6bo$25b3o9b58o$25bo
3bo8bo$27b3o9b56o$27b4o9bo$30bo10b54o$42bo$43b5obobb5obobob5obobb5obob
ob14o$44bo4bobobo3boobobbo4bobobo3boobobbo$45boo8boo3bo3boo8boo3bo3b
12o$46bobbo5b4o6bobbo5b4o6bo$47bobo8bobo5bobo8bobo5b10o$51bo8bo9bo8bo
6bo$51bo8boo8bo8boo6b8o$51boobo6b3o6boobo6b3o5bo$54bo8bo9bo8bo6b6o$90b
o$91b4o$92bo$93boo$94bo!

#C shift a greyship left or right edge in by one stripe
#C Jason Summers  5 Jul 2005
x = 77, y = 55, rule = B3/S23
77o$$77o$$77o$$77o$$56obobob5obobb5obo$56boobobbo4bobobo3boo$bb5obobob
5obobb5obobob3ob3obbooboboboboo3boo3bo3boo8boo$bobo3boobobbo4bobobo3b
oobobboobboobboo3bobbo4booboo6bobbo5b4o$5boo3bo3boo8boo3bo3bo3bo8bobb
3o3bobobo5bobo8bo$5b4o6bobbo5b4o5boobb6obo14bo9bo$8bobo5bobo8bobo3bobo
8bo4b3o7boo8bo$bo8bo9bo8bo3booboobboo7bo3bo6b3o6boobo$bo8boo8bo8boo3b
3o3bo3boboobbo3bo7bo9bo$boobo6b3o6boobo5boo7bobboobo6boobo$4bo8bo9bo5b
o5b3o$27bobo3boo$25b3o4boobo$24boobbo5bo$26bo5bo$24bobo5bobo$24bo6bo$
21b4o7bobo$21boo9bo$19bo14bo4bobo$19b4o9b3o3bobbo$18bo12b3o3boo$17b3o
bbo9boo$18b3o12b8o$19bo14bobo4bo$20b3obo12b3o$20bobboo12bo3bo$21b3o15b
3o$23bo15b4o$21bo20bo$21bobo$20bo$21bobo$21bo$23bo$21b3o$20bobboo$20b
3obo$19bo$18b3o$17b3obbo$18bo$19b4o$19bo$21boo$21b4o$24bo!

#C  Greyship with slope of 5/9  Hartmut Holzwart  5 Jul 2005
x = 140, y = 115, rule = B3/S23
68bo$65b4o$65b3o$63bo3bo$63b3o10boo$61bo5bo7booboo$61b6o6bob5o$59bo10b
obobooboo$59b12oboboo$57bo16boo$57b18o9b4o$55bo19bo7bo4bo$55b20o7bo$
53bo23bobobo6bo$53b27o$51bo42boo$51b32o10b4o$49bo34bo7b5o$49b35o7bo$
47bo38boboo$47b40oboo$45bo44bo11bobbo$45b46o10bo$7bo35bo57bo3bo$4b4o
35b50o8b4o$4boo35bo53bob3o$bbo38b55obobo$bb4o33bo59bo$bo37b61o10boo$3o
bbo31bo71booboo$b3o33b64o6bob5o$bbo32bo68bobobooboo$3b3obo27b70oboboo$
3bobboo25bo74boo$4b3o26b76o9b4o$6bo24bo77bo7bo4bo$4bo26b78o7bo$4bobo
22bo81bobobo6bo$3bo25b85o$4bobo20bo100boo$4bo22b90o10b4o$6bo18bo92bo7b
5o$4b3o18b93o7bo$3bobboo15bo96boboo$3b3obo15b98oboo$bbo18bo102bo11bobb
o$b3o17b104o10bo$3obbo13bo115bo3bo$bo17b108o8b4o$bb4o11bo111bob3o$bbo
14b113obobo$4boo9bo117bo$4b4obo5b119o$7boobobbo$9boobb122o$10boo126bo$
11b128o$$11b128o$10boo126bo$9boobb122o$7boobobbo$4b4obo5b119o$4boo9bo
117bo$bbo14b113obobo$bb4o11bo111bob3o$bo17b108o8b4o$3obbo13bo115bo3bo$
b3o17b104o10bo$bbo18bo102bo11bobbo$3b3obo15b98oboo$3bobboo15bo96boboo$
4b3o18b93o7bo$6bo18bo92bo7b5o$4bo22b90o10b4o$4bobo20bo100boo$3bo25b85o
$4bobo22bo81bobobo6bo$4bo26b78o7bo$6bo24bo77bo7bo4bo$4b3o26b76o9b4o$3b
obboo25bo74boo$3b3obo27b70oboboo$bbo32bo68bobobooboo$b3o33b64o6bob5o$
3obbo31bo71booboo$bo37b61o10boo$bb4o33bo59bo$bbo38b55obobo$4boo35bo53b
ob3o$4b4o35b50o8b4o$7bo35bo57bo3bo$45b46o10bo$45bo44bo11bobbo$47b40ob
oo$47bo38boboo$49b35o7bo$49bo34bo7b5o$51b32o10b4o$51bo42boo$53b27o$53b
o23bobobo6bo$55b20o7bo$55bo19bo7bo4bo$57b18o9b4o$57bo16boo$59b12oboboo
$59bo10bobobooboo$61b6o6bob5o$61bo5bo7booboo$63b3o10boo$63bo3bo$65b3o$
65b4o$68bo!

#C some components for a possible p4 greyship traveling perpendicular
#C  to its stripes, instead of parallel  Jason Summers  5 July 2005
x = 209, y = 93, rule = B3/S23
186b3o3b3o$186bobbobobbo$186bo7bo$186bo7bo$73b3o3b3o5b3o3b3o91bobobobo
$59bo5bo6bobbo3bobbo3bobbo3bobbo6bo5bo77bobobobo$58b3o3b3o5bo3bobo3bo
3bo3bobo3bo5b3o3b3o77bo3bo$43b3o3b3o5bobbooboobbo3bobbobobobo3bo3bobob
obobbo3bobbooboobbo5b3o3b3o61b3ob3o$29bo5bo7bobbobobbo4b3obbobobbobob
5obobbob7obobbob5obobobbobobb3o4bobbobobbo7bo5bo50bo$28b3o3b3o4bo4bobo
3bobbo3bobobobo3bo29bo3bobobobo3bobbo3bobo4bo4b3o3b3o45b9o$13b3o3b3o5b
oobbobobboo3b4obobob10obbob41obobb10obobob4o3boobbobobboo5b3o3b3o29bo
9bo$12bobbo3bobbo3bobbobobobo8bobobo71bobobo8bobobobobbo3bobbo3bobbo
27b13o$12bo3bobo3bo3b4obobobb10ob75ob10obbobob4o3bo3bobo3bo26bo13bo$
11bobbobobobo3bo6bo105bo6bo3bobobobobbo24b17o$10b5obobbob127obobbob5o
22bo17bo$9bo149bo20b21o$9b151o19bo21bo$178b25o$9b151o17bo25bo$176b29o$
9b151o15bo29bo$174b33o$9b151o13bo33bo$172b37o11$8bo3b8o$3bo3b5o8bo$bb
3obbo4b8o$bobboobobboo$boo4bobobb8o$4boobooboo8bo$3b4oboobb8o$oobboobo
3bo$9boob8o$11bo8bo$9bobb8o$9b3o$8bo3b8o$3bo3b5o8bo$bb3obbo4b8o$bobboo
bobboo$boo4bobobb8o$4boobooboo8bo$3b4oboobb8o$oobboobo3bo$9boob8o$11bo
8bo$9bobb8o$9b3o$8bo3b8o$3bo3b5o8bo$bb3obbo4b8o$bobboobobboo$boo4bobo
bb8o$4boobooboo8bo$3b4oboobb8o$oobboobo3bo$9boob8o$11bo8bo$9bobb8o$9b
3o$8bo3b8o$3bo3b5o8bo$bb3obbo4b8o$bobboobobboo$boo4bobobb8o$4boobooboo
8bo19b73o$3b4oboobb8o$oobboobo3bo28b73o$9boob8o$11bo8bo19b73o$9bobb8o$
9b3o28b73o$8bo3b8o$3bo3b5o8bo19b35obob35o$bb3obbo4b8o52bobobobobo$bobb
oobobboo28b27obo15bob27o$boo4bobobb8o44bobobo15bobobo$4boobooboo8bo19b
19obo31bob19o$3b4oboobb8o36bobobo31bobobo$oobboobo3bo28b11obo47bob11o$
9boob8o28bobobo47bobobo$11bo8bo19b3obo63bob3o$9bobb8o20bobobo63bobobo!

A structured pattern for a Caterpillar

Structured patterns

Something I've been wanting to do for a while now is to produce a structured description of Gabriel Nivasch's Caterpillar.

In the context of the Game of Life, a "structured pattern" would be a description in terms of the smaller subpatterns that are repeated many times in the full pattern, such as the "shish-ke-babs" or the various rakes that make up the Caterpillar. The subpatterns in turn may be composed of smaller sub-subpatterns like pi climbers, blinkers, gliders, etc. A structured format makes a much better "blueprint" of a large pattern than a standard RLE encoding or picture-format file, and it's also very compact -- probably better compression than any standard binary-archive tool could manage.

Xlife 3.5/3.6 provides a good pattern format for describing this kind of structured pattern. Unfortunately it isn't quite versatile enough for this purpose. The big problem is that when you're dealing with periodic subpatterns, you often want to be able to include copies of them at several different phases. Xlife's approach is to define one phase of each periodic pattern as its "base" pattern; to paste multiple copies in, you paste the first base pattern, run the entire universe some number of generations to get the first pattern to the right phase relative to the second; then paste the second base pattern -- and if necessary run N more generations and paste a third base pattern, and so forth.

For stable patterns, or patterns that don't interact too closely, that's fine. But unfortunately this approach doesn't work very well for large numbers of subpatterns or higher periods -- sometimes Xlife's format doesn't support a "natural" compact definition based on subpatterns, because (for example) two of the subpatterns interfere with each other before the correct phase of the third subpattern can be placed to stabilize the whole conglomeration.

Ideas for an extension of Xlife #I format:

First, for reference, here is a summary of current Xlife syntax.

An extension of the format would fix the problem described above -- you'd have to be able to say, "run just this pattern in isolation for N generations, then paste it at (x,y)." This seems like a more natural way to compose patterns from subpatterns.

-- In fact, that's how Xlife's GUI does it! To register subpatterns in a "load script", you specify subpatterns' locations, transformations, and number of ticks forward in time from the base pattern. It's actually quite a surprise to look in an #I-format file for the first time and find out that Xlife has translated your registered subpatterns into this alternate format that is only sometimes equivalent.

I think Eugene Langvagen's PLife project has the necessary versatility to describe this kind of run-N-ticks-then-paste operation, but I haven't done enough benchmarking yet to know whether PLife can handle Caterpillar-sized structured patterns.

The main problem that I see is that a PLife script can easily become much too syntactically complex to be read directly by other Life software. You could create a structured pattern using a PLife script, but you'd have to convert it back to RLE to communicate it to anyone who doesn't have Python and PLife available. Xlife format is much more straightforward to write a parser for.

2c/3 transceiver, large size

The new 2c/3 receiver accepts diagonal signals from the track and uses a repeatable reaction to convert these signals into output gliders. (In the pattern as shown below, all the output gliders are blocked, but one or more of them could easily be allowed to escape by removing the appropriate eaters.)

This version of the receiver can process signals separated by 2175 or more generations. The incoming signal interacts with a small constellation of still lifes at the receiver end of the 2c/3 track (two blocks and an eater, shown in light green in the picture). With the assistance of a few catalysts, the constellation collapses cleanly into an R-pentomino, which is then guided onto a Herschel track.

The path of the active signal is shown in gray the image below; the direction of travel is indicated by the red arrows. Gliders from the output Herschel (short blue arrows) are used to create two more Herschels; the Herschels are then routed to various Herschel-to-glider converters, which produce five gliders in two salvos (long blue arrows). Four of these gliders collide to rebuild the original constellation. (The first glider just removes an extra block left by the conversion of the receiver's initial output R-pentomino to a Herschel.)

2c/3 signal receiver: Dave Greene, 6 February 2005

2c/3 details

2c/3 is a respectable speed in the Life universe; by comparison, a glider travels at only one-fourth of the speed of light, and it was proven many years ago that this is the fastest that any finite diagonal spaceship can travel through empty space. There is a similar limit of half of the speed of light for orthogonal spaceships.

However, disturbances in pre-existing structures can travel much faster than these limits -- there is no theoretical limit lower than lightspeed, either diagonally or orthogonally. See Gabriel Nivasch's lightspeed article for details and examples.

A signal in a 2c/3 track will quickly overtake a glider travelling in the same direction. If a sufficiently long track can be made to turn a corner, a 2c/3 signal in it will even overtake an orthogonal c/2 spaceship.