The Last Few Years of Life News

For the past few years, Heinrich Koenig has been making available an ongoing catalog of new Game of Life results and current open problems. [I've been helping out some, but it's his server, so he ends up doing most of the work...]

Some randomly selected highlights:

Based on a recent 41-cell construction by Bill Gosper that exhibits O(t ln t) growth, Nick Gotts produced a pattern with only 26 ON cells with O(t^2) growth. [Update based on Nick Gotts' comment: Gosper's 41-cell construction remains the smallest pattern with a growth rate that is not an integral power of t.]

Hartmut Holzwart spent a little time recently constructing strange some patterns that look like inside-out spaceships. They're actually signals that travel through a half-ON, half-OFF striped agar -- the pattern that serves as the center of most of Holzwart's recent extensible "greyship" spaceships. The new signals move at 2c/3, two thirds of the "speed of light", and at right angles to previously-known lightspeed signals in the same medium.

Speaking of 2c/3, a while back Noam Elkies and I put together a 2c/3 diagonal signal transceiver based on a "wire" designed by Dean Hickerson. A transceiver is a device capable of transmitting information along a variable-length "wire"; in this case, the signal travels diagonally at two thirds of the speed of light, faster than any possible spaceship-based signal.

For diagonal signalling, this can even beat Jason Summers' telegraph from February 2003, which can communicate along an orthogonal "wire" at the speed of light (see Gabriel Nivasch's discussion of lightspeed signals -- a pair of telegraphs at right angles can only manage c/2 diagonally.)

Nicolay Beluchenko, in addition to producing several incredible collections of new Game-of-Life spaceships with a variety of new shapes and speeds -- and has also modified a known 'Garden of Eden', or 'orphan' pattern to fit it into a 12x12 bounding box. [Update: Achim Flammenkamp had previously discovered a 12x11 Garden of Eden with only 72 ON cells.]

Along with his extended explorations of c/12 Cordership technology, David Bell created a series of new sawtooth patterns. Definition of 'sawtooth' from Stephen Silver's Life Lexicon: "Any finite pattern whose population grows without bound but does not tend to infinity. (In other words, the population reaches new heights infinitely often, but also infinitely often returns to some fixed value.)".

Dean Hickerson invented some new "transcendental patterns" consisting of puffers and guns, which grow in what appear to be unpredictable ways.

A little farther back (December of 2004) Gabriel Nivasch, in an incredible feat of Life engineering, put the finishing touches on a Caterpillar -- a spaceship that travels at the previously unknown speed of 17c/45.

Many of the above patterns are much easier to study now that Andrew Trevorrow and Tomas Rokicki have made available their new cross-platform Life simulator, "Golly". It works on Macintosh, Windows, and Linux boxes, and makes clever use of hash tables to display the evolution of patterns with interesting large-scale behavior to a previously unheard-of number of generations.

Before the Caterpillar appeared on the scene, Karel Suhajda, Scot Ellison, David Eppstein, Paul Chapman, and others collaborated on the project of completing Jason Summers' sub-1000 gun collection [download link] -- an impressive conglomeration of the smallest known patterns that produce one output glider every p generations, for each period p=14 to 999.

This "gun collection" showcases a surprising variety of Life patterns, since as a general rule most new primes or prime factors require different mechanisms! (Some patterns have adjustable periods, but adjusting them tends to increase their size... and quite soon a custom-designed alternative with a smaller bounding box can generally edge them out of the running.)

Most of the higher-period guns were produced with Karel Suhajda's search program 'Hersrch' [download link], which given a target period can automatically generate a minimal Herschel loop (standard period-independent signal-guiding Life technology, originated by David Buckingham and extended by Paul Callahan). But the gun collection is an apparently inexhaustible source of optimization problems: as new Life technology is discovered, it can be incorporated into new guns with smaller bounding boxes, as in the case of this new piece of Herschel technology.

Back in 2004, Paul Tooke discovered an amazing new Cordership with only three engines, much easier to construct with gliders than any of its predecessors -- see '/jslife/guns/gun-corder-p690.lif' in Jason Summers' patttern collection.

Mark Niemiec's incredible collection of glider constructions is always worth mentioning. He's been steadily adding to the collection with syntheses of new discoveries.

Also in 2004, Jared Prince made an ingenious modification to David Bell's old Unit Life Cell. His new "Deep Cell" can process two independent states in parallel, opening up the possibility of running an infinite number of infinite Life configurations simultaneously in a single infinite universe (it's just that most of the configurations are simulated very, very, very slowly...) But of course for this kind of proof-by-example, execution speed isn't really the point: the pudding is in the proof, not in the practical details -- or however one should phrase that.

---------------------------------------------

Number-theory curiosities of various kinds have been showing up in of Game of Life patterns for a long time, of course. Many Game of Life engineering efforts involve infinitely-expanding patterns -- ranging from mathematically simple ones like Hartmut Holzwart's MAX pattern, which expands at the maximum sustainable speed in all directions, to much more complex engineering efforts like Dean Hickerson's prime-number generator -- or Jason Summers' modification of Hickerson's pattern, which expands forever unless it discovers a new Fermat prime (!). In August 2003 Jason Summers constructed a pattern that expands at O(log n) -- and logic circuitry that can store and manipulate integer values in O(log n) space is also within reach now.

New results from Glue 2

Paul Chapman's Glue project is producing some interesting results these days. Glue (or rather Glue 2) is a search program that finds "natural" constructions of singlets (indivisible p1 and p2 patterns) by starting with a target object -- usually a block -- and bombarding it with a p2 slow salvo of gliders.

'salvo' means that all the gliders come from the same direction; 'slow' means that glider #n+1 must not arrive until the reaction from glider #n's collision has settled down into stability or a p2 oscillation, and 'p2' means that the only timing constraint on the gliders is that an even or odd phase may be specified. (Many intermediate collision results contain blinkers, beacons, toads, or other p2 patterns, and a glider on a given input lane can interact with a p2 target in two possible ways.)

You can also download the RLE, or have a look at a larger image. Here are the actual recipes in text format, and the MCell file used to create the above picture.

This is an example of a clever new MCell rule by Brice Due -- it shows not only the Smear but also the starting locations of the gliders and block, without changing anything about how Life actually evolves. Potentially a fairly useful trick for displaying this stuff. His notes also taught me a new way to do cell-state substitutions, with an MCell command I hadn't noticed (or at least realized the potential of). I had been doing the same task much more painfully by setting up whole new rules to do state conversions.

After the pattern is run, the full cell history is visible, just as in MCell's 'HistoricalLife' rule: all cells that were ON at any point during the reaction are blue instead of black --

Here's another take on the same display problem: Koenig's annotation format allows for multiple layers in different colors, in a format that's backwards compatible with standard RLE (at least for most Life editors.) Click on the image to see the RLE:

Finally, here's a screenshot of the current version of the Glue 2 search program used to generate these recipes:

Holiday Greyships -- Grey No Longer!

Over the last several months, Hartmut Holzwart (with some help and suggestions from Jason Summers and others) has been building a wide variety of "greyships": extensible orthogonal spaceships with a wide variety of sizes and shapes, where the expandable central area is made up of stripes -- half ON and half OFF cells, either parallel or perpendicular to the spaceship's direction of travel.

Running these ships in MCell with the Rainbow024 palette and 17 alive states (see the Colors menu for both settings) gave some nice Yuletide colors -- figured I'd post the results here:

trial pattern showing a slipping-stripe reaction sent in
by Gabriel Nivasch: Hartmut Holzwart, 21 November 2005

alternate mirror-symmetric pattern showing Gabriel Nivasch's
slipping-stripe reaction: Hartmut Holzwart, 28 November 2005

hybrid 2c/4 greyship: Hartmut Holzwart, 16 November 2005

alternate hybrid 2c/4 greyship
Hartmut Holzwart, 16 November 2005

sample asymmetric hybrid greyship
Hartmut Holzwart, 18 November 2005

hybrid greyship: Hartmut Holzwart, 18 November 2005

symmetric hybrid greyship: Hartmut Holzwart, 18 November 2005

triangular hybrid greyship:
Hartmut Holzwart, 23 Nov 2005

greyship showing new components: Hartmut Holzwart, 25 Nov 2005

hybrid greyship with a crooked internal boundary
Hartmut Holzwart, 8 December 2005

asymmetrical c/3 greyship
Hartmut Holzwart, 11 November 2005

long and short c/3 ships w/ central p14 wick,
based on a ship from Jason Summers' raw c/3 collection:
Hartmut Holzwart, 14 Nov 2005

c/3 ship with central p15/5 wick: Hartmut Holzwart, 7 Decenber 2005

perpendicular-to-the-grain greyship with new back slope
Hartmut Holzwart, 29 November 2005

new greyship component shown on right side
Hartmut Holzwart, 29 November 2005

mirror-symmetric against-the-grain greyship with new back slopes
Hartmut Holzwart, 2005-11-30

perpendicular greyship with -1/4 back slope
Hartmut Holzwart, 1 Dec 2005

pentagonal perpendicular greyship with -1/4 back slope
Hartmut Holzwart, 1 Dec 2005

sample greyship-based puffer:
Hartmut Holzwart, 2 Dec 2005

perpendicular greyship with even symmetry --
new back slope, front end from a spacefiller:
Hartmut Holzwart, 5 December 2005

two even-symmetry perpendicular
greyships chained together, with
small tagalongs at back end:
Hartmut Holzwart, 5 December 2005

new perpendicular greyship with central
wick from an old unfinished spacefiller:
Hartmut Holzwart, 6 December 2005

perpendicular greyship with -1/2 back slope
Hartmut Holzwart, 7 December 2005

greyships suggested by Gabriel Nivasch,
with stripes offset by one down the middle:
Hartmut Holzwart, 7 December 2005

Some ideas for a p8 or pure-stable Unit Life Cell

I've been looking a little bit at rebuilding David Bell's Unit Life Cell using p4/p8 glider and Herschel technology. The point would be to produce a unitcell with a period that's a power of two, to work more efficiently with hashlife/qlife algorithms. The p30 mechanisms in the current unitcell mean that hashlife has to add 15 different phases to its hash table before it has them all (I think). Also, I was wondering if it might not be possible to squash the necessary p8 circuitry into a 256x256 area -- or [much more likely!] into a 256x512 area, which hashlife could handle just about as well. The idea is to optimize the design for simulation by the new hashlife-based player/editor, Golly:

http://golly.sourceforge.net

I think the Life-logic circuitry can be simplified considerably if the neighbor-count chute is modified a bit; in particular, if the stream of gliders that reads the contents of the chute is slowed down to (let's say) p64, then it's possible to check that either the #2 or the #3 neighbor-count glider is the first one out of the chute -- and then suppress the #2 neighbor-count glider with a negated cell-is-ON signal.

With a long-enough gap between gliders, Herschel-based switches can allow just the first glider of a stream to get through, then automatically reset itself afterwards. Here's one such circuit that works at p64:

Okay, now imagine a Unit Life Cell with no moving parts. An infinite grid of OFF unitcells will just sit there; it takes three appropriately-timed gliders from neighboring unitcells to activate a given cell, and then it stays activated only as long as two or three gliders keep coming in to sustain it.

A glider at some critical spot still means the unitcell is ON, and the lack of that glider means that it's OFF.

As in the p8 case, the fanout device is simple to construct with Herschel circuitry -- it could be a standard G->H converter (fairly compact at p8, but not too bad even at p1) followed by a string of glider-producing conduits:

Then the trouble starts. If the unitcell can't have any moving parts, there can't be a "timing gun" in it saying when to look for gliders from neighboring cells. So we have to always produce a "timing" signal at exactly the same time no matter which gliders come in from neighboring cells -- one glider, two gliders, eight gliders.

I have the feeling that I'm not being clever enough, but the best design I can think of at the moment is a string of eight circuits like the following sample pattern, each hooked up to an input glider from a neighboring cell:

Then you also have to actually count the number of signals from neighboring cells. Luckily the above pattern has a spare output glider for each input signal, and these could be collected into a single lane with standard stable reflectors and sent through a counting mechanism. Here's one possibility:

#C ladder from programmable constructor --
#C could be used as a configurable neighbor-counting mechanism
x = 424, y = 465, rule = B3/S23
207bo$207b3o$210bo$191bo17boo$179bo11b3o$177b3o14bo$161bo14bo16boo$
161b3o12boo$164bo$163boo3$164boo$164boo17boo$183boo$$221boo$221boo3$
180boo$180bo19boo$181b3o15bobo$183bo15bo$177boo19boo$177bo$178b3o$180b
o6$186boo$186bo$167boo15bobo$167boo15boo$155boo$154bobo$154bo$153boo$
47bo9bo$47b3o5b3o27bo$37boo11bo3bo30b3o$16bo19bobo10boo3boo32bo14bo$
17bo18bo50boo12b3o$15b3o17boo63bo$100boo$166boo$165bobo$99boo64bo$80b
oo17boo63boo$32boo46boo$bboo28boo$3bo$3o$o$$83boo$63boo19bo$43bo6boo
11bobo15b3o92boo$41b3o6boo13bo15bo94boo$40bo24boo19boo$40boo45bo$84b3o
$84bo$$165boo107bo$166bo19boo86b3o$102boo62bobo17bo90bo$78bo23bobo62b
oo15bobo71bo17boo$78b3o23bo74bo4boo60bo11b3o$81bo22boo72bobo63b3o14bo$
80boo14boo80bobo47bo14bo16boo$96boo69boo10bo48b3o12boo$166bobo62bo$
166bo63boo$165boo$180boo$180bo50boo$181b3o47boo17boo$183bo66boo$$288b
oo$288boo$$97boo$97bobo147boo$99bo147bo19boo$99boo147b3o15bobo$250bo
15bo$244boo19boo$244bo$245b3o$247bo4$87boo$87boo$253boo$253bo$96boo
136boo15bobo$96boo136boo15boo$222boo$221bobo$221bo$220boo$95boo17bo9bo
$95bo18b3o5b3o27bo$91boo3b3o5boo11bo3bo30b3o$91bobo4bo4bobo10boo3boo
32bo14bo$93bo9bo50boo12b3o$62boo29boo7boo63bo$61bobo103boo$61bo4boo
165boo$60boo5bo164bobo$64b3o99boo64bo$64bo82boo17boo63boo$99boo46boo$
69boo28boo$70bo$67b3o$67bo$$150boo$130boo19bo$110bo6boo11bobo15b3o92b
oo$108b3o6boo13bo15bo94boo$107bo24boo19boo$107boo45bo$151b3o$151bo$$
232boo$233bo19boo90boo$169boo62bobo17bo91boo$145bo23bobo62boo15bobo71b
o$145b3o23bo74bo4boo60bo11b3o$148bo22boo72bobo63b3o14bo$147boo14boo80b
obo47bo14bo16boo$163boo69boo10bo48b3o12boo$233bobo62bo$233bo63boo$232b
oo$247boo$247bo50boo$248b3o47boo17boo$250bo66boo$$355boo$355boo$$164b
oo$164bobo147boo$166bo147bo19boo$166boo147b3o15bobo$317bo15bo$311boo
19boo$311bo$312b3o$314bo4$154boo$154boo$320boo$320bo$163boo136boo15bob
o$163boo136boo15boo$289boo$288bobo$288bo$287boo$162boo17bo9bo$162bo18b
3o5b3o27bo$158boo3b3o5boo11bo3bo30b3o$158bobo4bo4bobo10boo3boo32bo14bo
$160bo9bo50boo12b3o$129boo29boo7boo63bo$128bobo103boo$128bo4boo165boo$
127boo5bo164bobo$131b3o99boo64bo$131bo82boo17boo63boo$166boo46boo$136b
oo28boo$137bo$134b3o$134bo$$217boo$197boo19bo$177bo6boo11bobo15b3o92b
oo$175b3o6boo13bo15bo94boo$174bo24boo19boo$174boo45bo$218b3o$218bo$$
299boo107bo$300bo19boo86b3o$236boo62bobo17bo90bo$212bo23bobo62boo15bob
o71bo17boo$212b3o23bo74bo4boo60bo11b3o$215bo22boo72bobo63b3o14bo$214b
oo14boo80bobo47bo14bo16boo$230boo69boo10bo48b3o12boo$300bobo62bo$300bo
63boo$299boo$314boo$314bo50boo$315b3o47boo17boo$317bo66boo$$422boo$
422boo$$231boo$231bobo147boo$233bo147bo19boo$233boo147b3o15bobo$384bo
15bo$378boo19boo$378bo$379b3o$381bo4$221boo$221boo$387boo$387bo$230boo
136boo15bobo$230boo136boo15boo$356boo$355bobo$355bo$354boo$229boo17bo
9bo$229bo18b3o5b3o27bo$225boo3b3o5boo11bo3bo30b3o$225bobo4bo4bobo10boo
3boo32bo14bo$227bo9bo50boo12b3o$196boo29boo7boo63bo$195bobo103boo$195b
o4boo165boo$194boo5bo164bobo$198b3o99boo64bo$198bo82boo17boo63boo$233b
oo46boo$203boo28boo$204bo$201b3o$201bo$$284boo$264boo19bo$244bo6boo11b
obo15b3o92boo$242b3o6boo13bo15bo94boo$241bo24boo19boo$241boo45bo$285b
3o$285bo$$366boo$367bo19boo$303boo62bobo17bo$279bo23bobo62boo15bobo$
279b3o23bo74bo4boo$282bo22boo72bobo$281boo14boo80bobo$297boo69boo10bo$
367bobo$367bo$366boo$381boo$381bo$382b3o$384bo5$298boo$298bobo$300bo$
300boo9$288boo$288boo3$297boo$297boo5$296boo17bo9bo$296bo18b3o5b3o27bo
$292boo3b3o5boo11bo3bo30b3o$292bobo4bo4bobo10boo3boo32bo14bo$294bo9bo
50boo12b3o$263boo29boo7boo63bo$262bobo103boo$262bo4boo$261boo5bo$265b
3o99boo$265bo82boo17boo$300boo46boo$270boo28boo$271bo$268b3o$268bo$$
351boo$331boo19bo$311bo6boo11bobo15b3o$309b3o6boo13bo15bo$308bo24boo
19boo$308boo45bo$352b3o$352bo4$370boo$346bo23bobo$346b3o23bo$349bo22b
oo$348boo14boo$364boo12$365boo$365bobo$367bo$367boo9$355boo$355boo3$
364boo$364boo5$363boo$363bo$359boo3b3o$359bobo4bo$361bo$330boo29boo$
329bobo$329bo4boo$287bo40boo5bo$285b3o44b3o$284bo47bo25boo$284boo53boo
17bobo$269boo67bobo19bo$270bo67bo21boo$270bobo6bo57boo$271boo4bobo3bo$
278boobbobo$282bobo$283bo4boo$271boo15bobo$270bobo17bo65boo$270bo19boo
64bo$269boo86b3o$359bo$294boo$294bo$292bobo$292boo46boo$280boo57bobo$
280boo57bo$338boo7$348boo$268boo78boo$269bo$269bobo83bo$270boo83b3o$
358bo$357boo$337boo$338bo$338bobo$339boo3$353boo$353bobo$355bo$271boo
15boo65boo$271boo15bobo$263boo25bo$264bo25boo$264bobo$265boo$$350boo$
350bo$284bo66b3o$282b3o68bo$281bo$281boo20bo$287bo15b3o$285b3o18bo$
284bo20boo11boo$284boo32boo6$287boo37boo21boo$268boo17boo36bobo21boo$
268boo55bo17boo$324boo17boo$$267boo$268bo76boo$265b3o12boo56boo5boo$
265bo14bo16boo39boo$281b3o14bo$283bo11b3o20boo$295bo22bo$319b3o$321bo!

Because there's a separate output for each possible neighbor count (if the ladder were extended to eight "rungs") it's possible to add eaters to block off outputs corresponding to any standard Bnnn.../Snnn... rule. The remaining outputs would be collected into a single lane with standard stable reflectors, as before -- the ladder would be set up so that there's at most one output glider for any neighbor-count (and either an ON or OFF cell-state signal, which suppresses either the S or B part of the ladder's output signal.)

The size of the ladder means that 512^2 is probably too small to hold the entire stable pattern -- but the next larger power of two, 1024^2, should be plenty big enough. And it should be relatively easy to adjust the period of the cell to a power of two, as well: probably p8192.

David Bell's Unit Life Cell adjusted to 512^2

There's a new cross-platform open-source Life editor in the works -- and an insurmountable opportunity came up recently in the "golly-test" discussion list. Brice Due had constructed several patterns made up of "unit Life cells", which are large Life logic circuit configurations that mimic the behavior of single Life cells. Thus a single infinite Life universe can support an infinite regress of unitcells simulating unitcells simulating unitcells, at exponentially slower speeds. (See also Jared Prince's "Deep Cell".)

As it turns out, the timing guns in David Bell's original 500x500 Unit Life Cell are a good bit slower than they need to be, so there's still plenty of time for signals to arrive from neighboring 512-size cells, even though they have a little farther to travel. So the biggest headache was resynchronizing a lot of p30 circuitry; stretching each unitcell by 12 cells added multiples of 48 ticks to the glider paths. [If only the magic number had been 515 instead of 512, I would hardly have had to resynchronize anything at all...]

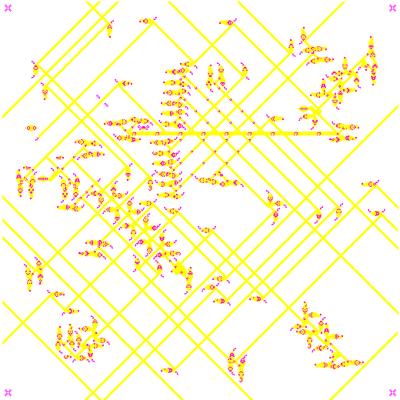The "circuit diagram" for the original Unit Life Cell is shown at right: the area is 499^2 cells (and you need a one-cell-wide space between adjacent cells).

I didn't include a trail for the reaction for an OFF cell with two neighbors, which makes use of the isolated pentadecathlon at the left -- the #2 neighbor-count glider bounces back and annihilates what would otherwise be the ON output glider generated by the #3 neighbor-count glider. (I think.)

I had to make surprisingly few changes to expand the above to a 511^2 cell -- basically, just a gun and a few reflectors in the lower left corner had to be moved southwest, and then the gun, the counting chute, and all the reflectors leading to it needed to be rephased to match the new timing of the gliders from neighboring cells.

Here's the RLE for a single 511^2 Unit Life Cell.

-- And here's the RLE for a 3x3 test grid representing a blinker, with the Xlife version here.

Coincidentally, I had to switch to RLE in the unitcell #B definition -- it looks like the current version of Xlife can't quite handle picture-format subpatterns at width 512, so my 3x3 grid was getting corrupted. I included the #M prefix in the RLE header, so Achim's Xlife 3.6 should be able to handle the above pattern. I have a private build (3.5.2. going on 3.5.3) that can handle RLE subpatterns with or without the non-standard Xlife-style #M tags, but that change hasn't spread very far yet...

------------------------------------

It wouldn't be an impossibly difficult task to adjust the unitcell period to be a power of 2 as well: after David Bell designed and built the original Unit Life Cell, a p8N glider reflector was discovered, comparable in size to the p30N reflector used in the current unitcell. (Unlike p30, p8 would be compatible with power-of-two step sizes between generations, which would match the way Golly's underlying 'hlife' algorithm works with Life patterns.]

However, so far I am successfully resisting that project: since the fanout device and the glider-to-block converters (and the rest of the neighbor-counting logic) are irrecoverably p30, they'd all have to be replaced with p8 equivalents -- and offhand I don't know of a p8 glider-to-block converter or a small alternate glider reflector equivalent to the two-p30-gun reflector used to get gliders onto the other square color. Easy enough to arrange a new Herschel-based fanout device so no alternate reflectors are needed, though --

Rather than work on a p8-reflector-based version, I'd be tempted to find a pure-stable solution: the advantage would be that any cells that are not ON have no moving parts whatsoever! Which would probably increase the simulation speed, and might also make it easier to see the active cells in a large pattern of unitcells. I think I have all the pieces for a pure-stable Unit Life Cell worked out in my head now (see the next posting)... and they are even easy to reconfigure for any standard rule. Well, any non-B0 rule at least -- otherwise I need a clock gun in each cell.

Sawtooth pattern needs tuneup

[thumbnail at .5 sub-pixel zoom -- click on image to expand]

attempted sawtooth pattern with incorrect timing --
runs for three cycles and then blows up.
The generations where the line burns out to
create a block are 3648, 9952, 20896, and 39800.
Their remainders modulo 192 are 0, 160, 160, and 56.
The growth in the generation numbers is
approximately a factor of 1.72.

David Bell, 18 July 2005

Adapted from notes by David Bell:

For the sawtooth to be made functional, the remainders of the generation numbers where the line burns out (modulo 192) must either be constant or else oscillate only over a few "safe" values.

The sawtooth can be easily modified by shifting the glider reflectors forwards or backwards along the path and by adjusting when the beehive is turned into the backward glider. But simply bouncing the gliders back using the glider reflectors might not be good enough; it might be necessary to hold onto them until the right generation numbers before releasing them.

Alternative sawtooth mechanism

David Bell, 18 July 2005

Another sawtooth mechanism: a pair of gliders can arrive from the end of the line to cleanly ignite it while sending a glider back to the source direction. Perhaps the timings involved in this alternative mechanism would be easier:

Update: 16 August 2005

another attempted sawtooth with incorrect timing --
runs for about 342,000 ticks and then blows up.
A p1056 gun is attached to a p8 regulator
in place of the original simple reflectors.
Dave Greene, 16 August 2005

Notes by Dave Greene:
I tried replacing the reflectors at the stationary end of the pattern with a p8 universal regulator, and ended up with an almost-sawtooth that works nicely for 342,000 generations -- and then blows up. Apparently my math is still wrong somewhere...

My one useful result was that a line-igniting glider can be delayed by any multiple of 176 generations, and the burning fuse will still arrive at the active site at the same phase of the p192 lineship. [After 192 generations the fuse is longer by 16 cells, so it takes 16 ticks longer to burn. So to keep the burning fuse from arriving late at the active site, you have to subtract 16 ticks from 192].

-- So I attached a p1056 gun (6 x 176) to the universal regulator, and found a configuration that survives for quite a few cycles... apparently by sheer luck, since there's something wrong with the underlying theory. The problem seems to be that the ever-increasing return time of the glider also extends the length of the fuse by a variable amount -- and the fuse burns four times as fast as a glider travels, so it's easy for the feedback effect to result in several possible arrival times. The burning-out reaction is versatile enough to handle any amount of lateness up to 80 ticks or so after the phase used for the first couple of cycles -- but eventually a phase always seems to come along that is off by more than that.

I also tried p880 and p2112 drive guns [I thought I had accounted for the variable fuse lengths with p2112, which is LCM(176,192) -- but no such luck.] It seems possible that delaying one of these drive guns by some number of generations would get the pattern into a stable cycle -- I just haven't figured out how to predict this in advance yet, and brute-force searching is fairly tedious in this case. Anyway, it wouldn't be quite as interesting to get the right answer by accident!

I tried writing equations to predict the length of later cycles, given the glider travel time and fuse burning time and the phase of the burning fuse's arrival at the active site... but so far I've always ended up with wrong answers after a cycle or two. Haven't given up yet, but would be happy if someone else wanted to figure it out!