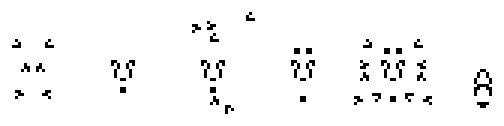Reposted with permission from
Alexey Nigin's blog:
The day before yesterday (March 6, 2016)
ConwayLife.com forums saw a new member named
zdr. When we the lifenthusiasts meet a newcomer, we expect to see things like “brand new” 30-cell 700-gen
methuselah and then have to explain why it is not notable. However, what zdr showed us made our jaws drop.
It was a 28-cell
c/10 orthogonal spaceship:

To explain why this is such a groundbreaking discovery, I should first tell you that Life spaceships can be loosely divided into two categories.
Engineered ships are the ones that consist of various small components. They often have adjustable
speed. However, the population of
tens of thousands to
millions of cells causes these spaceships to have no practical value.
There is much more incentive in hunting for
elementary spaceships, which can be used for complex constructions. They are found using programs such as gfind or WLS. The algorithms behind these programs are beyond the scope of my article, but the important thing is that the search time goes up exponentially as the
period of the ship grows. It is most interesting to find spaceships of new speeds, and the number of speeds that low-period ships can have is unfortunately limited:
|
Orthogonal |
Diagonal |
| c/2 |
Yes |
Impossible |
| c/3 |
Yes |
Impossible |
| c/4 |
Yes |
Yes |
| c/5 |
Yes |
Yes |
| 2c/5 |
Yes |
Impossible |
| c/6 |
Yes |
Yes |
| c/7 |
Yes |
Yes |
| 2c/7 |
Yes |
Impossible |
| 3c/7 |
No |
Impossible |
| c/8 |
No |
No |
| 3c/8 |
No |
Impossible |
This table does not include oblique speeds, which causes little inconvenience because no elementary oblique ships are known.
The table above shows that ships exist for most of possible speeds, and it seems obvious that the speeds for which there are no ships have been searched by numerous people with good knowledge of search programs, powerful computers and lots of patience. As for higher periods, even the smallest searches would take years on modern computers. It appears that low-hanging fruit have been harvested clean during the 46 years of Life research… or, more precisely, it
appeared so before zdr’s post.
The idea we all missed is that if the ship is really microscopic, it can be found in reasonable time despite its high period. After zdr boldly went where no man has gone before, Josh Ball set up the
corresponding search in gfind and refound the spaceship in a little over an hour. zdr
said that their program found it in a matter of 19 seconds.
To be frank, similar event did happen before when the aforementioned Josh Ball
pulled loafer out of a hat. However, zdr’s spaceship (which is now called
Copperhead, as
proposed by muzik) is much more awesome for a number of reasons:
- Loafer is not so mind-bogglingly high-period.
- Copperhead was much easier to find, so it is more surprising that nobody found it before.
- Copperhead’s tail is relatively strong and can interact with other objects without breaking down.
The discovery of a new spaceship speed immediately opened a few new areas of research, which are being explored now.
Synthesis
Aidan F. Pierce
came up with a Copperhead
synthesis only 10 hours after the completion of the spaceship. The synthesis was inefficient, and a few people discovered better ones. The
current best synthesis, made by Chris Cain, requires only 22 gliders. Its repeat time is 375 ticks, which means that a gun can start constructing the second spaceship 375 ticks after the first one. There is a 23-glider synthesis with a better repeat time of 373 ticks.
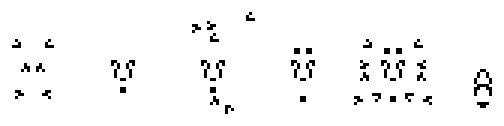
The synthesis can be substantially improved if we find this spaceship crawling out of a random soup. Adam P. Goucher has written a wonderful program called
apgsearch, which is perfectly suited for this task. While the current version may be too slow to find a soup in reasonable time, highly anticipated version 3.0 can probably do the trick. Once it is found, it will appear
here.
Guns
Once the synthesis was complete, building a gun was nothing but
corollary-sniping. The
first copperhead gun was created by myself, and a video of it is available
here. It was put together in a hurry and is therefore extremely inefficient. In particular, skilled gun builders can spot a silly mistake in the Northeast.
gmc_nxtman then made
another gun with an almost optimal period of 376 ticks.
Eaters
simeks found
two eaters for this ship, the better of which is shown below:

It is now time to search for a good copperhead-to-something-useful converter. The
only existing one is clumsy and slow.
Sawtooths
Sawtooths often work by sending a flotilla of fast ships towards a slower ship. The more is the difference in speed, the less is the expansion factor of a sawtooth. Since expansion factor is proportional to how boring the sawtooth is, increasing the speed difference is a good thing. Dean Hickerson collided c/2 standard spaceships with c/10 copperhead to get a
sawtooth with expansion factor 6:
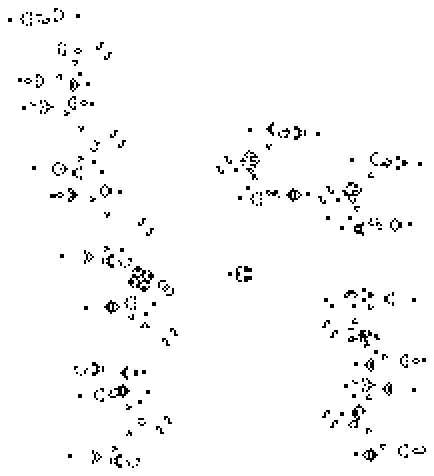
He then made
another sawtooth with expansion factor 10/3.
Puffers and rakes
Suppose a c/10 flotilla is hit by a glider. The glider turns into loads of mess, but all copperheads somehow survive and move on. The mess releases a glider, which flies into strategically placed second flotilla that is identical to the first one. Gliders continue to bounce back and forth between flotillas leaving mess behind them, and a c/10 puffer is complete!
Unfortunately, this cool technique doesn’t work out easily in our case. There are no interesting interactions between a glider and a single copperhead, and it is unclear how one can place two or more copperheads so close to each other that a glider interacts with all of them. Assuming we figure it out, we can try to make a rake by perturbing the mess with copperheads so that it evolves into gliders, but that seems even less likely.
However, all this hand-waving can be turned it real puffers if we find…
Tagalongs
Tagalongs are small things that are attached to the back of a spaceship and move with it. Here is an example tagalong, called the
Schick engine:

Finding a tagalong for the copperhead (or two copperheads) will be really nice. We can also try searching for pushalongs, but they are generally rarer.
Other patterns
There are a few other areas of Life exploration where the copperhead can be useful. For example,
universal constructors often need to create an elbow still life very far away. It can be done by producing a copperhead, waiting for some time, and then shooting the copperhead down with a LWSS. At the moment I do not see why the copperhead can be better than the loafer in this aspect, but who knows?