Holiday Greyships -- Grey No Longer!

Over the last several months, Hartmut Holzwart (with some help and suggestions from Jason Summers and others) has been building a wide variety of "greyships": extensible orthogonal spaceships with a wide variety of sizes and shapes, where the expandable central area is made up of stripes -- half ON and half OFF cells, either parallel or perpendicular to the spaceship's direction of travel.

Running these ships in MCell with the Rainbow024 palette and 17 alive states (see the Colors menu for both settings) gave some nice Yuletide colors -- figured I'd post the results here:

trial pattern showing a slipping-stripe reaction sent in
by Gabriel Nivasch: Hartmut Holzwart, 21 November 2005

alternate mirror-symmetric pattern showing Gabriel Nivasch's
slipping-stripe reaction: Hartmut Holzwart, 28 November 2005

hybrid 2c/4 greyship: Hartmut Holzwart, 16 November 2005

alternate hybrid 2c/4 greyship
Hartmut Holzwart, 16 November 2005

sample asymmetric hybrid greyship
Hartmut Holzwart, 18 November 2005

hybrid greyship: Hartmut Holzwart, 18 November 2005

symmetric hybrid greyship: Hartmut Holzwart, 18 November 2005

triangular hybrid greyship:
Hartmut Holzwart, 23 Nov 2005

greyship showing new components: Hartmut Holzwart, 25 Nov 2005

hybrid greyship with a crooked internal boundary
Hartmut Holzwart, 8 December 2005

asymmetrical c/3 greyship
Hartmut Holzwart, 11 November 2005

long and short c/3 ships w/ central p14 wick,
based on a ship from Jason Summers' raw c/3 collection:
Hartmut Holzwart, 14 Nov 2005

c/3 ship with central p15/5 wick: Hartmut Holzwart, 7 Decenber 2005

perpendicular-to-the-grain greyship with new back slope
Hartmut Holzwart, 29 November 2005

new greyship component shown on right side
Hartmut Holzwart, 29 November 2005

mirror-symmetric against-the-grain greyship with new back slopes
Hartmut Holzwart, 2005-11-30

perpendicular greyship with -1/4 back slope
Hartmut Holzwart, 1 Dec 2005

pentagonal perpendicular greyship with -1/4 back slope
Hartmut Holzwart, 1 Dec 2005

sample greyship-based puffer:
Hartmut Holzwart, 2 Dec 2005

perpendicular greyship with even symmetry --
new back slope, front end from a spacefiller:
Hartmut Holzwart, 5 December 2005

two even-symmetry perpendicular
greyships chained together, with
small tagalongs at back end:
Hartmut Holzwart, 5 December 2005

new perpendicular greyship with central
wick from an old unfinished spacefiller:
Hartmut Holzwart, 6 December 2005

perpendicular greyship with -1/2 back slope
Hartmut Holzwart, 7 December 2005

greyships suggested by Gabriel Nivasch,
with stripes offset by one down the middle:
Hartmut Holzwart, 7 December 2005

Some ideas for a p8 or pure-stable Unit Life Cell

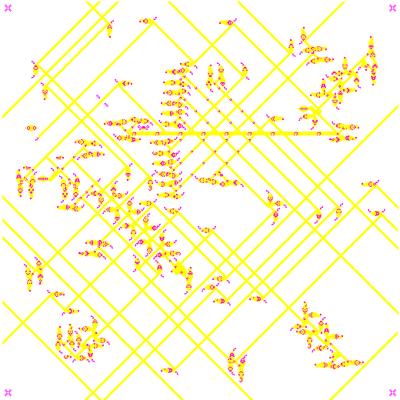
I've been looking a little bit at rebuilding David Bell's Unit Life Cell using p4/p8 glider and Herschel technology. The point would be to produce a unitcell with a period that's a power of two, to work more efficiently with hashlife/qlife algorithms. The p30 mechanisms in the current unitcell mean that hashlife has to add 15 different phases to its hash table before it has them all (I think). Also, I was wondering if it might not be possible to squash the necessary p8 circuitry into a 256x256 area -- or [much more likely!] into a 256x512 area, which hashlife could handle just about as well. The idea is to optimize the design for simulation by the new hashlife-based player/editor, Golly:

http://golly.sourceforge.net

I think the Life-logic circuitry can be simplified considerably if the neighbor-count chute is modified a bit; in particular, if the stream of gliders that reads the contents of the chute is slowed down to (let's say) p64, then it's possible to check that either the #2 or the #3 neighbor-count glider is the first one out of the chute -- and then suppress the #2 neighbor-count glider with a negated cell-is-ON signal.

With a long-enough gap between gliders, Herschel-based switches can allow just the first glider of a stream to get through, then automatically reset itself afterwards. Here's one such circuit that works at p64:

Okay, now imagine a Unit Life Cell with no moving parts. An infinite grid of OFF unitcells will just sit there; it takes three appropriately-timed gliders from neighboring unitcells to activate a given cell, and then it stays activated only as long as two or three gliders keep coming in to sustain it.

A glider at some critical spot still means the unitcell is ON, and the lack of that glider means that it's OFF.

As in the p8 case, the fanout device is simple to construct with Herschel circuitry -- it could be a standard G->H converter (fairly compact at p8, but not too bad even at p1) followed by a string of glider-producing conduits:

Then the trouble starts. If the unitcell can't have any moving parts, there can't be a "timing gun" in it saying when to look for gliders from neighboring cells. So we have to always produce a "timing" signal at exactly the same time no matter which gliders come in from neighboring cells -- one glider, two gliders, eight gliders.

I have the feeling that I'm not being clever enough, but the best design I can think of at the moment is a string of eight circuits like the following sample pattern, each hooked up to an input glider from a neighboring cell:

Then you also have to actually count the number of signals from neighboring cells. Luckily the above pattern has a spare output glider for each input signal, and these could be collected into a single lane with standard stable reflectors and sent through a counting mechanism. Here's one possibility:

#C ladder from programmable constructor --
#C could be used as a configurable neighbor-counting mechanism
x = 424, y = 465, rule = B3/S23
207bo$207b3o$210bo$191bo17boo$179bo11b3o$177b3o14bo$161bo14bo16boo$
161b3o12boo$164bo$163boo3$164boo$164boo17boo$183boo$$221boo$221boo3$
180boo$180bo19boo$181b3o15bobo$183bo15bo$177boo19boo$177bo$178b3o$180b
o6$186boo$186bo$167boo15bobo$167boo15boo$155boo$154bobo$154bo$153boo$
47bo9bo$47b3o5b3o27bo$37boo11bo3bo30b3o$16bo19bobo10boo3boo32bo14bo$
17bo18bo50boo12b3o$15b3o17boo63bo$100boo$166boo$165bobo$99boo64bo$80b
oo17boo63boo$32boo46boo$bboo28boo$3bo$3o$o$$83boo$63boo19bo$43bo6boo
11bobo15b3o92boo$41b3o6boo13bo15bo94boo$40bo24boo19boo$40boo45bo$84b3o
$84bo$$165boo107bo$166bo19boo86b3o$102boo62bobo17bo90bo$78bo23bobo62b
oo15bobo71bo17boo$78b3o23bo74bo4boo60bo11b3o$81bo22boo72bobo63b3o14bo$
80boo14boo80bobo47bo14bo16boo$96boo69boo10bo48b3o12boo$166bobo62bo$
166bo63boo$165boo$180boo$180bo50boo$181b3o47boo17boo$183bo66boo$$288b
oo$288boo$$97boo$97bobo147boo$99bo147bo19boo$99boo147b3o15bobo$250bo
15bo$244boo19boo$244bo$245b3o$247bo4$87boo$87boo$253boo$253bo$96boo
136boo15bobo$96boo136boo15boo$222boo$221bobo$221bo$220boo$95boo17bo9bo
$95bo18b3o5b3o27bo$91boo3b3o5boo11bo3bo30b3o$91bobo4bo4bobo10boo3boo
32bo14bo$93bo9bo50boo12b3o$62boo29boo7boo63bo$61bobo103boo$61bo4boo
165boo$60boo5bo164bobo$64b3o99boo64bo$64bo82boo17boo63boo$99boo46boo$
69boo28boo$70bo$67b3o$67bo$$150boo$130boo19bo$110bo6boo11bobo15b3o92b
oo$108b3o6boo13bo15bo94boo$107bo24boo19boo$107boo45bo$151b3o$151bo$$
232boo$233bo19boo90boo$169boo62bobo17bo91boo$145bo23bobo62boo15bobo71b
o$145b3o23bo74bo4boo60bo11b3o$148bo22boo72bobo63b3o14bo$147boo14boo80b
obo47bo14bo16boo$163boo69boo10bo48b3o12boo$233bobo62bo$233bo63boo$232b
oo$247boo$247bo50boo$248b3o47boo17boo$250bo66boo$$355boo$355boo$$164b
oo$164bobo147boo$166bo147bo19boo$166boo147b3o15bobo$317bo15bo$311boo
19boo$311bo$312b3o$314bo4$154boo$154boo$320boo$320bo$163boo136boo15bob
o$163boo136boo15boo$289boo$288bobo$288bo$287boo$162boo17bo9bo$162bo18b
3o5b3o27bo$158boo3b3o5boo11bo3bo30b3o$158bobo4bo4bobo10boo3boo32bo14bo
$160bo9bo50boo12b3o$129boo29boo7boo63bo$128bobo103boo$128bo4boo165boo$
127boo5bo164bobo$131b3o99boo64bo$131bo82boo17boo63boo$166boo46boo$136b
oo28boo$137bo$134b3o$134bo$$217boo$197boo19bo$177bo6boo11bobo15b3o92b
oo$175b3o6boo13bo15bo94boo$174bo24boo19boo$174boo45bo$218b3o$218bo$$
299boo107bo$300bo19boo86b3o$236boo62bobo17bo90bo$212bo23bobo62boo15bob
o71bo17boo$212b3o23bo74bo4boo60bo11b3o$215bo22boo72bobo63b3o14bo$214b
oo14boo80bobo47bo14bo16boo$230boo69boo10bo48b3o12boo$300bobo62bo$300bo
63boo$299boo$314boo$314bo50boo$315b3o47boo17boo$317bo66boo$$422boo$
422boo$$231boo$231bobo147boo$233bo147bo19boo$233boo147b3o15bobo$384bo
15bo$378boo19boo$378bo$379b3o$381bo4$221boo$221boo$387boo$387bo$230boo
136boo15bobo$230boo136boo15boo$356boo$355bobo$355bo$354boo$229boo17bo
9bo$229bo18b3o5b3o27bo$225boo3b3o5boo11bo3bo30b3o$225bobo4bo4bobo10boo
3boo32bo14bo$227bo9bo50boo12b3o$196boo29boo7boo63bo$195bobo103boo$195b
o4boo165boo$194boo5bo164bobo$198b3o99boo64bo$198bo82boo17boo63boo$233b
oo46boo$203boo28boo$204bo$201b3o$201bo$$284boo$264boo19bo$244bo6boo11b
obo15b3o92boo$242b3o6boo13bo15bo94boo$241bo24boo19boo$241boo45bo$285b
3o$285bo$$366boo$367bo19boo$303boo62bobo17bo$279bo23bobo62boo15bobo$
279b3o23bo74bo4boo$282bo22boo72bobo$281boo14boo80bobo$297boo69boo10bo$
367bobo$367bo$366boo$381boo$381bo$382b3o$384bo5$298boo$298bobo$300bo$
300boo9$288boo$288boo3$297boo$297boo5$296boo17bo9bo$296bo18b3o5b3o27bo
$292boo3b3o5boo11bo3bo30b3o$292bobo4bo4bobo10boo3boo32bo14bo$294bo9bo
50boo12b3o$263boo29boo7boo63bo$262bobo103boo$262bo4boo$261boo5bo$265b
3o99boo$265bo82boo17boo$300boo46boo$270boo28boo$271bo$268b3o$268bo$$
351boo$331boo19bo$311bo6boo11bobo15b3o$309b3o6boo13bo15bo$308bo24boo
19boo$308boo45bo$352b3o$352bo4$370boo$346bo23bobo$346b3o23bo$349bo22b
oo$348boo14boo$364boo12$365boo$365bobo$367bo$367boo9$355boo$355boo3$
364boo$364boo5$363boo$363bo$359boo3b3o$359bobo4bo$361bo$330boo29boo$
329bobo$329bo4boo$287bo40boo5bo$285b3o44b3o$284bo47bo25boo$284boo53boo
17bobo$269boo67bobo19bo$270bo67bo21boo$270bobo6bo57boo$271boo4bobo3bo$
278boobbobo$282bobo$283bo4boo$271boo15bobo$270bobo17bo65boo$270bo19boo
64bo$269boo86b3o$359bo$294boo$294bo$292bobo$292boo46boo$280boo57bobo$
280boo57bo$338boo7$348boo$268boo78boo$269bo$269bobo83bo$270boo83b3o$
358bo$357boo$337boo$338bo$338bobo$339boo3$353boo$353bobo$355bo$271boo
15boo65boo$271boo15bobo$263boo25bo$264bo25boo$264bobo$265boo$$350boo$
350bo$284bo66b3o$282b3o68bo$281bo$281boo20bo$287bo15b3o$285b3o18bo$
284bo20boo11boo$284boo32boo6$287boo37boo21boo$268boo17boo36bobo21boo$
268boo55bo17boo$324boo17boo$$267boo$268bo76boo$265b3o12boo56boo5boo$
265bo14bo16boo39boo$281b3o14bo$283bo11b3o20boo$295bo22bo$319b3o$321bo!

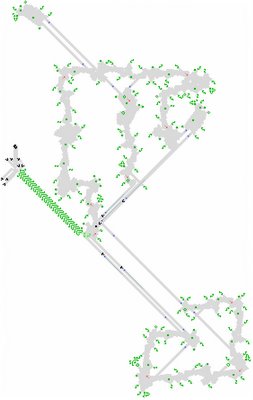
Because there's a separate output for each possible neighbor count (if the ladder were extended to eight "rungs") it's possible to add eaters to block off outputs corresponding to any standard Bnnn.../Snnn... rule. The remaining outputs would be collected into a single lane with standard stable reflectors, as before -- the ladder would be set up so that there's at most one output glider for any neighbor-count (and either an ON or OFF cell-state signal, which suppresses either the S or B part of the ladder's output signal.)

The size of the ladder means that 512^2 is probably too small to hold the entire stable pattern -- but the next larger power of two, 1024^2, should be plenty big enough. And it should be relatively easy to adjust the period of the cell to a power of two, as well: probably p8192.

David Bell's Unit Life Cell adjusted to 512^2

There's a new cross-platform open-source Life editor in the works -- and an insurmountable opportunity came up recently in the "golly-test" discussion list. Brice Due had constructed several patterns made up of "unit Life cells", which are large Life logic circuit configurations that mimic the behavior of single Life cells. Thus a single infinite Life universe can support an infinite regress of unitcells simulating unitcells simulating unitcells, at exponentially slower speeds. (See also Jared Prince's "Deep Cell".)

As it turns out, the timing guns in David Bell's original 500x500 Unit Life Cell are a good bit slower than they need to be, so there's still plenty of time for signals to arrive from neighboring 512-size cells, even though they have a little farther to travel. So the biggest headache was resynchronizing a lot of p30 circuitry; stretching each unitcell by 12 cells added multiples of 48 ticks to the glider paths. [If only the magic number had been 515 instead of 512, I would hardly have had to resynchronize anything at all...]

The "circuit diagram" for the original Unit Life Cell is shown at right: the area is 499^2 cells (and you need a one-cell-wide space between adjacent cells).

I didn't include a trail for the reaction for an OFF cell with two neighbors, which makes use of the isolated pentadecathlon at the left -- the #2 neighbor-count glider bounces back and annihilates what would otherwise be the ON output glider generated by the #3 neighbor-count glider. (I think.)

I had to make surprisingly few changes to expand the above to a 511^2 cell -- basically, just a gun and a few reflectors in the lower left corner had to be moved southwest, and then the gun, the counting chute, and all the reflectors leading to it needed to be rephased to match the new timing of the gliders from neighboring cells.

Here's the RLE for a single 511^2 Unit Life Cell.

-- And here's the RLE for a 3x3 test grid representing a blinker, with the Xlife version here.

Coincidentally, I had to switch to RLE in the unitcell #B definition -- it looks like the current version of Xlife can't quite handle picture-format subpatterns at width 512, so my 3x3 grid was getting corrupted. I included the #M prefix in the RLE header, so Achim's Xlife 3.6 should be able to handle the above pattern. I have a private build (3.5.2. going on 3.5.3) that can handle RLE subpatterns with or without the non-standard Xlife-style #M tags, but that change hasn't spread very far yet...

------------------------------------

It wouldn't be an impossibly difficult task to adjust the unitcell period to be a power of 2 as well: after David Bell designed and built the original Unit Life Cell, a p8N glider reflector was discovered, comparable in size to the p30N reflector used in the current unitcell. (Unlike p30, p8 would be compatible with power-of-two step sizes between generations, which would match the way Golly's underlying 'hlife' algorithm works with Life patterns.]

However, so far I am successfully resisting that project: since the fanout device and the glider-to-block converters (and the rest of the neighbor-counting logic) are irrecoverably p30, they'd all have to be replaced with p8 equivalents -- and offhand I don't know of a p8 glider-to-block converter or a small alternate glider reflector equivalent to the two-p30-gun reflector used to get gliders onto the other square color. Easy enough to arrange a new Herschel-based fanout device so no alternate reflectors are needed, though --

Rather than work on a p8-reflector-based version, I'd be tempted to find a pure-stable solution: the advantage would be that any cells that are not ON have no moving parts whatsoever! Which would probably increase the simulation speed, and might also make it easier to see the active cells in a large pattern of unitcells. I think I have all the pieces for a pure-stable Unit Life Cell worked out in my head now (see the next posting)... and they are even easy to reconfigure for any standard rule. Well, any non-B0 rule at least -- otherwise I need a clock gun in each cell.

Sawtooth pattern needs tuneup

[thumbnail at .5 sub-pixel zoom -- click on image to expand]

attempted sawtooth pattern with incorrect timing --
runs for three cycles and then blows up.
The generations where the line burns out to
create a block are 3648, 9952, 20896, and 39800.
Their remainders modulo 192 are 0, 160, 160, and 56.
The growth in the generation numbers is
approximately a factor of 1.72.

David Bell, 18 July 2005

Adapted from notes by David Bell:

For the sawtooth to be made functional, the remainders of the generation numbers where the line burns out (modulo 192) must either be constant or else oscillate only over a few "safe" values.

The sawtooth can be easily modified by shifting the glider reflectors forwards or backwards along the path and by adjusting when the beehive is turned into the backward glider. But simply bouncing the gliders back using the glider reflectors might not be good enough; it might be necessary to hold onto them until the right generation numbers before releasing them.

Alternative sawtooth mechanism

David Bell, 18 July 2005

Another sawtooth mechanism: a pair of gliders can arrive from the end of the line to cleanly ignite it while sending a glider back to the source direction. Perhaps the timings involved in this alternative mechanism would be easier:

Update: 16 August 2005

another attempted sawtooth with incorrect timing --
runs for about 342,000 ticks and then blows up.
A p1056 gun is attached to a p8 regulator
in place of the original simple reflectors.
Dave Greene, 16 August 2005

Notes by Dave Greene:
I tried replacing the reflectors at the stationary end of the pattern with a p8 universal regulator, and ended up with an almost-sawtooth that works nicely for 342,000 generations -- and then blows up. Apparently my math is still wrong somewhere...

My one useful result was that a line-igniting glider can be delayed by any multiple of 176 generations, and the burning fuse will still arrive at the active site at the same phase of the p192 lineship. [After 192 generations the fuse is longer by 16 cells, so it takes 16 ticks longer to burn. So to keep the burning fuse from arriving late at the active site, you have to subtract 16 ticks from 192].

-- So I attached a p1056 gun (6 x 176) to the universal regulator, and found a configuration that survives for quite a few cycles... apparently by sheer luck, since there's something wrong with the underlying theory. The problem seems to be that the ever-increasing return time of the glider also extends the length of the fuse by a variable amount -- and the fuse burns four times as fast as a glider travels, so it's easy for the feedback effect to result in several possible arrival times. The burning-out reaction is versatile enough to handle any amount of lateness up to 80 ticks or so after the phase used for the first couple of cycles -- but eventually a phase always seems to come along that is off by more than that.

I also tried p880 and p2112 drive guns [I thought I had accounted for the variable fuse lengths with p2112, which is LCM(176,192) -- but no such luck.] It seems possible that delaying one of these drive guns by some number of generations would get the pattern into a stable cycle -- I just haven't figured out how to predict this in advance yet, and brute-force searching is fairly tedious in this case. Anyway, it wouldn't be quite as interesting to get the right answer by accident!

I tried writing equations to predict the length of later cycles, given the glider travel time and fuse burning time and the phase of the burning fuse's arrival at the active site... but so far I've always ended up with wrong answers after a cycle or two. Haven't given up yet, but would be happy if someone else wanted to figure it out!

Perpendicular greyship update

Update: 22 July 2005 07:22

Hartmut Holzwart has produced some new partial results related to perpendicular greyships -- i.e., spaceships whose central section is made up of alternating lines of ON and OFF cells, and whose direction of travel is perpendicular to these lines. Several completed spaceships of this type are shown in an upcoming weblog posting.

Connection of 1/10 slope to 1/2 slope
Hartmut Holzwart, 14 July 2005

A 1/10-slope edge can be connected to a 1/2-slope edge:

Connection from side of perpendicular 
greyship to 1/4-slope back edge

Hartmut Holzwart, 22 July 2005

Jason Summers' side component can be connected to the 1/4 back edge component; however, Holzwart reports that his attempts to connect the side component to a known front component have not been successful.

Greyship details

Jul 1:

#C diamond-shaped greyship  Hartmut Holzwart  1 Jul 2005
x = 88, y = 83, rule = B3/S23
50bobo$49bobbo$48boo$47bo3bo$46b3obo$45bo$44b7o$5bobo35bo9boboo$4bobbo
34b12ob3o$3boo36bo16bo$bbo37b17obbo$b4o34bo19boo$o4bo32b23o$obbo33bo
21bo$obbo32b23o$bo33bo25boboo$bb4obo26b28ob3o$3bo3bo25bo32bo$4bo27b33o
bbo$4bobo24bo35boo$30b39o$3b3o23bo37bo$3boo23b39o$3b3o21bo41boboo$26b
44ob3o$4bobo18bo48bo$4bo19b49obbo$3bo3bo15bo51boo$bb4obo14b55o$bo19bo
53bo$obbo16b55o$obbo15bo57boboo$o4bo12b60ob3o$b4o12bo64bo$bbo13b65obbo
$3boo10bo67boo$4bobbobo4b71o$5bobobbobbo69bo$8bo3b71o$9bo75bobo$10b76o
bo$$10b76obo$9bo75bobo$8bo3b71o$5bobobbobbo69bo$4bobbobo4b71o$3boo10bo
67boo$bbo13b65obbo$b4o12bo64bo$o4bo12b60ob3o$obbo15bo57boboo$obbo16b
55o$bo19bo53bo$bb4obo14b55o$3bo3bo15bo51boo$4bo19b49obbo$4bobo18bo48bo
$26b44ob3o$3b3o21bo41boboo$3boo23b39o$3b3o23bo37bo$30b39o$4bobo24bo35b
oo$4bo27b33obbo$3bo3bo25bo32bo$bb4obo26b28ob3o$bo33bo25boboo$obbo32b
23o$obbo33bo21bo$o4bo32b23o$b4o34bo19boo$bbo37b17obbo$3boo36bo16bo$4bo
bbo34b12ob3o$5bobo35bo9boboo$44b7o$45bo$46b3obo$47bo3bo$48boo$49bobbo$
50bobo!

July 2:

#C front and sides for square greyship  Jason Summers 2 Jul 2005
x = 46, y = 63, rule = B3/S23
10bo$$10bo$$10bo4$8bo3bo$8bo3b27o$9bo$10b29o$$10b29o$9bo$8bo3b27o$8bo
3bo$8bo3b27o$9bo$10b29o$$10b29o$9bo$8bo3b27o$8bo3bo$8bo3b27o$9bo$10b
29o$$10b29o$9bo$8bo3b5obobb5obobob5obo$5bobobbobbo4bobobo3boobobbo4bo$
4bobbobo4boo8boo3bo3boo6bobobo$3boo10bobbo5b4o6bobbo$bbo13bobo8bobo5bo
bo$b4o15bo8bo$o4bo14bo8boo$obbo16boobo6b3o$obbo19bo8bo$bo$bb4obo$3bo3b
o$4bo$4bobo$$3b3o$3boo$3b3o$$4bobo$4bo$3bo3bo$bb4obo$bo$obbo$obbo$o4bo
$b4o$bbo$3boo$4bobbo$5bobo!

July 4:

#C 2c/4 45-90-45 triangle greyship  Hartmut Holzwart  4 Jul 2005
x = 100, y = 59, rule = S23/B3
48bobo$47bobbo$46boo$45bo3bo$44b3obo$7bo35bo$4b4o35b6o$4boo35bo9boboo$
bbo38b11ob3o$bb4o33bo16bo$bo37b16obbo$3obbo31bo19boo$b3o33b22o$bbo32bo
21bo$3b3obo27b22o$3bobboo25bo25boboo$4b3o26b27ob3o$6bo24bo32bo$4bo26b
32obbo$4bobo22bo35boo$3bo25b38o$4bobo20bo37bo$4bo22b38o$6bo18bo41boboo
$4b3o18b43ob3o$3bobboo15bo48bo$3b3obo15b48obbo$bbo18bo51boo$b3o17b54o$
3obbo13bo53bo$bo17b54o$bb4o11bo57boboo$bbo14b59ob3o$4boo9bo64bo$4b4obo
5b64obbo$7boobobbo67boo$9boobb70o$10boo69bo$11b70o10b3o3bo$83booboobb
7obbo$9b75o10bobboo$8boo78b3o6boo$7boobb3obb4obb4obb4obb4obb4obb4obb4o
bb4obb4obb4obb4obboobbobbo$6b3obb3obobboobobboobobboobobboobobboobobb
oobobboobobboobobboobobboobobboobobboo$7bobo7bo5bo5bo5bo5bo5bo5bo5bo5b
o5bo5bo5bo7b4o$8b3o80bo3bo$7bobboo79bo$10b3obbo76bobbo$10b3obbo$4boo7b
o$3boob5oboo$4b6ob3obo$5b3o3bobb3oboboo$13booboboo$11bo9boo$9boobbob3o
bobboboo$9bo4bobbobobooboo$9bo3boo5b3obo$10b3o7boo!

#C 45-90-45-triangle greyship with p2 technology except on backslope
#C Hartmut Holzwart  4 Jul 2005
x = 85, y = 74, rule = B3/S23
48bobo$47bobbo$46boo$45bo3bo$44b3obo$7bo35bo$4b4o35b6o$4boo35bo9boboo$
bbo38b11ob3o$bb4o33bo16bo$bo37b16obbo$3obbo31bo19boo$b3o33b22o$bbo32bo
21bo$3b3obo27b22o$3bobboo25bo25boboo$4b3o26b27ob3o$6bo24bo32bo$4bo26b
32obbo$4bobo22bo35boo$3bo25b38o$4bobo20bo37bo$4bo22b38o$6bo18bo41boboo
$4b3o18b43ob3o$3bobboo15bo48bo$3b3obo15b48obbo$bbo18bo51boo$b3o17b54o$
3obbo13bo53bo$bo17b54o$bb4o11bo57boboo$bbo14b59ob3o$4boo9bo64bo$4b4obo
5b64obbo$7boobobbo67boo$9boobb70o$10boo69bo$11b70o$$13b70obo$12boo69b
oo$11boobb4obobob5obobb5obobob5obobb5obobob5obobb5obobob3o$9boobobbo3b
oobobbo4bobobo3boobobbo4bobobo3boobobbo4bobobo3boobobboo$6b4obo5boo3bo
3boo8boo3bo3boo8boo3bo3boo8boo3bo$6boo9b4o6bobbo5b4o6bobbo5b4o6bobbo5b
4o$4bo15bobo5bobo8bobo5bobo8bobo5bobo8bobo$4b4o14bo9bo8bo9bo8bo9bo8bo$
3bo18boo8bo8boo8bo8boo8bo8boo$bb3obbo15b3o6boobo6b3o6boobo6b3o6boobo6b
3o$3b3o19bo9bo8bo9bo8bo9bo8bo$4bo$5b3obo$5bobboo$6b3o$8bo$6bo$6bobo$5b
o$6bobo$6bo$8bo$6b3o$5bobboo$5b3obo$4bo$3b3o$bb3obbo$3bo$4b4o$4bo$6boo
$6b4o$9bo!

#C greyship w/ back at limit slope ~1/4  Hartmut Holzwart  4 Jul 2005
x = 95, y = 120, rule = B3/S23
50bobo$49bobbo$48boo$47bo4bo$46b4obbo$45bo$45b3obobboo$7bo35bo6bobo$4b
4o35b8obbo$4boo35bo10bobo$bbo38b11obbo$bb4o33bo14boboo$bo37b14obobo$3o
bbo31bo16bobo$b3o33b18obo$bbo32bo18boboboo$3b3obo27b19obbo$3bobboo25bo
20boboboo$4b3o26b21obbobo$6bo24bo24boboo$4bo26b24obobo$4bobo22bo26bobo
$3bo25b28obo$4bobo20bo28boboboo$4bo22b29obbo$6bo18bo30boboboo$4b3o18b
31obbobo$3bobboo15bo34boboo$3b3obo15b34obobo$bbo18bo36bobo$b3o17b38obo
$3obbo13bo38boboboo$bo17b39obbo$bb4o11bo40boboboo$bbo14b41obbobo$4boo
9bo44boboo$4b4obo5b44obobo$7boobobbo46bobo$9boobb48obo$10boo48boboboo$
11b49obbo$60boboboo$11b49obbobo$10boo50boboo$9boobb48obobo$7boobobbo
48bobo$4b4obo5b48obo$4boo9bo46boboboo$bbo14b45obbo$bb4o11bo44boboboo$b
o17b43obbobo$3obbo13bo44boboo$b3o17b42obobo$bbo18bo42bobo$3b3obo15b42o
bo$3bobboo15bo40boboboo$4b3o18b39obbo$6bo18bo38boboboo$4bo22b37obbobo$
4bobo20bo38boboo$3bo25b36obobo$4bobo22bo36bobo$4bo26b36obo$6bo24bo34bo
boboo$4b3o26b33obbo$3bobboo25bo32boboboo$3b3obo27b31obbobo$bbo32bo32bo
boo$b3o33b30obobo$3obbo31bo30bobo$bo37b30obo$bb4o33bo28boboboo$bbo38b
27obbo$4boo35bo26boboboo$4b4o35b25obbobo$7bo35bo26boboo$45b24obobo$45b
o24bobo$47b24obo$47bo22boboboo$49b21obbo$49bo20boboboo$51b19obbobo$51b
o20boboo$53b18obobo$53bo18bobo$55b18obo$55bo16boboboo$57b15obbo$57bo
14boboboo$59b13obbobo$59bo14boboo$61b12obobo$61bo12bobo$63b12obo$63bo
10boboboo$65b9obbo$65bo8boboboo$67b7obbobo$67bo8boboo$69b6obobo$69bo6b
obo$71b6obo$71bo4bobobobo$73b3obbo3bo$73bobbo5boo$75bo4boob3obbo$74bo
3bobo3b3obo$74b3o6bobo$72boobo6boobo$71boboboo4boobooboobobo$71bobb3o
5bo4bo$71booboo7b4o3bobbo$73boo10bo4boobo$$91boo$89bo4bo$88bo$88bo5bo$
88b6o!

Jul 5:

#C junctions to construct arbitrary greyship front-edge slopes, 0-90
#C Jason Summers  5 Jul 2005
x = 95, y = 66, rule = B3/S23
9bobo17b30o$8bobbo18bo$7boo22b28o$6bo3bo21bo$5b3obo23b26o$bboo30bo$bo
3b5o25b24o$o3bo31bo$o5boo29b22o$3o3b4o28bo$bo7bo29b20o$boo37bo$bobo23b
obo4bobo4b18o$boobboobo8bobo6bobboboobobbo4bo$bbob3obo3bob4obobo3boo8b
o7b16o$9booboboobbobbobbo4bo6bobboobbo$4b6oboo3b4obob5obo7b4obboobb12o
$5bo4b3o6bo11boo10boobo$6boo5boobboobbob5obo7b4obboobb12o$7bobbo5b4obo
bbo4bo6bobboobbo$8boboboo5bobo3boo8bo7b16o$26bobboboobobbo4bo$27bobo4b
obo4b18o$40bo$39b20o$38bo$37b22o$36bo$35b24o$34bo$33b26o$32bo$31b28o$
30bo$29b30o$26boo$25bo3b30o$24bo3bo$24bo5b29o$24b3o3bo$25bobo4b63o$25b
oobbobbo$23bo3boo4b62o$22boo10bo$23b6o6b60o$24bo4bo6bo$25b3o9b58o$25bo
3bo8bo$27b3o9b56o$27b4o9bo$30bo10b54o$42bo$43b5obobb5obobob5obobb5obob
ob14o$44bo4bobobo3boobobbo4bobobo3boobobbo$45boo8boo3bo3boo8boo3bo3b
12o$46bobbo5b4o6bobbo5b4o6bo$47bobo8bobo5bobo8bobo5b10o$51bo8bo9bo8bo
6bo$51bo8boo8bo8boo6b8o$51boobo6b3o6boobo6b3o5bo$54bo8bo9bo8bo6b6o$90b
o$91b4o$92bo$93boo$94bo!

#C shift a greyship left or right edge in by one stripe
#C Jason Summers  5 Jul 2005
x = 77, y = 55, rule = B3/S23
77o$$77o$$77o$$77o$$56obobob5obobb5obo$56boobobbo4bobobo3boo$bb5obobob
5obobb5obobob3ob3obbooboboboboo3boo3bo3boo8boo$bobo3boobobbo4bobobo3b
oobobboobboobboo3bobbo4booboo6bobbo5b4o$5boo3bo3boo8boo3bo3bo3bo8bobb
3o3bobobo5bobo8bo$5b4o6bobbo5b4o5boobb6obo14bo9bo$8bobo5bobo8bobo3bobo
8bo4b3o7boo8bo$bo8bo9bo8bo3booboobboo7bo3bo6b3o6boobo$bo8boo8bo8boo3b
3o3bo3boboobbo3bo7bo9bo$boobo6b3o6boobo5boo7bobboobo6boobo$4bo8bo9bo5b
o5b3o$27bobo3boo$25b3o4boobo$24boobbo5bo$26bo5bo$24bobo5bobo$24bo6bo$
21b4o7bobo$21boo9bo$19bo14bo4bobo$19b4o9b3o3bobbo$18bo12b3o3boo$17b3o
bbo9boo$18b3o12b8o$19bo14bobo4bo$20b3obo12b3o$20bobboo12bo3bo$21b3o15b
3o$23bo15b4o$21bo20bo$21bobo$20bo$21bobo$21bo$23bo$21b3o$20bobboo$20b
3obo$19bo$18b3o$17b3obbo$18bo$19b4o$19bo$21boo$21b4o$24bo!

#C  Greyship with slope of 5/9  Hartmut Holzwart  5 Jul 2005
x = 140, y = 115, rule = B3/S23
68bo$65b4o$65b3o$63bo3bo$63b3o10boo$61bo5bo7booboo$61b6o6bob5o$59bo10b
obobooboo$59b12oboboo$57bo16boo$57b18o9b4o$55bo19bo7bo4bo$55b20o7bo$
53bo23bobobo6bo$53b27o$51bo42boo$51b32o10b4o$49bo34bo7b5o$49b35o7bo$
47bo38boboo$47b40oboo$45bo44bo11bobbo$45b46o10bo$7bo35bo57bo3bo$4b4o
35b50o8b4o$4boo35bo53bob3o$bbo38b55obobo$bb4o33bo59bo$bo37b61o10boo$3o
bbo31bo71booboo$b3o33b64o6bob5o$bbo32bo68bobobooboo$3b3obo27b70oboboo$
3bobboo25bo74boo$4b3o26b76o9b4o$6bo24bo77bo7bo4bo$4bo26b78o7bo$4bobo
22bo81bobobo6bo$3bo25b85o$4bobo20bo100boo$4bo22b90o10b4o$6bo18bo92bo7b
5o$4b3o18b93o7bo$3bobboo15bo96boboo$3b3obo15b98oboo$bbo18bo102bo11bobb
o$b3o17b104o10bo$3obbo13bo115bo3bo$bo17b108o8b4o$bb4o11bo111bob3o$bbo
14b113obobo$4boo9bo117bo$4b4obo5b119o$7boobobbo$9boobb122o$10boo126bo$
11b128o$$11b128o$10boo126bo$9boobb122o$7boobobbo$4b4obo5b119o$4boo9bo
117bo$bbo14b113obobo$bb4o11bo111bob3o$bo17b108o8b4o$3obbo13bo115bo3bo$
b3o17b104o10bo$bbo18bo102bo11bobbo$3b3obo15b98oboo$3bobboo15bo96boboo$
4b3o18b93o7bo$6bo18bo92bo7b5o$4bo22b90o10b4o$4bobo20bo100boo$3bo25b85o
$4bobo22bo81bobobo6bo$4bo26b78o7bo$6bo24bo77bo7bo4bo$4b3o26b76o9b4o$3b
obboo25bo74boo$3b3obo27b70oboboo$bbo32bo68bobobooboo$b3o33b64o6bob5o$
3obbo31bo71booboo$bo37b61o10boo$bb4o33bo59bo$bbo38b55obobo$4boo35bo53b
ob3o$4b4o35b50o8b4o$7bo35bo57bo3bo$45b46o10bo$45bo44bo11bobbo$47b40ob
oo$47bo38boboo$49b35o7bo$49bo34bo7b5o$51b32o10b4o$51bo42boo$53b27o$53b
o23bobobo6bo$55b20o7bo$55bo19bo7bo4bo$57b18o9b4o$57bo16boo$59b12oboboo
$59bo10bobobooboo$61b6o6bob5o$61bo5bo7booboo$63b3o10boo$63bo3bo$65b3o$
65b4o$68bo!

#C some components for a possible p4 greyship traveling perpendicular
#C  to its stripes, instead of parallel  Jason Summers  5 July 2005
x = 209, y = 93, rule = B3/S23
186b3o3b3o$186bobbobobbo$186bo7bo$186bo7bo$73b3o3b3o5b3o3b3o91bobobobo
$59bo5bo6bobbo3bobbo3bobbo3bobbo6bo5bo77bobobobo$58b3o3b3o5bo3bobo3bo
3bo3bobo3bo5b3o3b3o77bo3bo$43b3o3b3o5bobbooboobbo3bobbobobobo3bo3bobob
obobbo3bobbooboobbo5b3o3b3o61b3ob3o$29bo5bo7bobbobobbo4b3obbobobbobob
5obobbob7obobbob5obobobbobobb3o4bobbobobbo7bo5bo50bo$28b3o3b3o4bo4bobo
3bobbo3bobobobo3bo29bo3bobobobo3bobbo3bobo4bo4b3o3b3o45b9o$13b3o3b3o5b
oobbobobboo3b4obobob10obbob41obobb10obobob4o3boobbobobboo5b3o3b3o29bo
9bo$12bobbo3bobbo3bobbobobobo8bobobo71bobobo8bobobobobbo3bobbo3bobbo
27b13o$12bo3bobo3bo3b4obobobb10ob75ob10obbobob4o3bo3bobo3bo26bo13bo$
11bobbobobobo3bo6bo105bo6bo3bobobobobbo24b17o$10b5obobbob127obobbob5o
22bo17bo$9bo149bo20b21o$9b151o19bo21bo$178b25o$9b151o17bo25bo$176b29o$
9b151o15bo29bo$174b33o$9b151o13bo33bo$172b37o11$8bo3b8o$3bo3b5o8bo$bb
3obbo4b8o$bobboobobboo$boo4bobobb8o$4boobooboo8bo$3b4oboobb8o$oobboobo
3bo$9boob8o$11bo8bo$9bobb8o$9b3o$8bo3b8o$3bo3b5o8bo$bb3obbo4b8o$bobboo
bobboo$boo4bobobb8o$4boobooboo8bo$3b4oboobb8o$oobboobo3bo$9boob8o$11bo
8bo$9bobb8o$9b3o$8bo3b8o$3bo3b5o8bo$bb3obbo4b8o$bobboobobboo$boo4bobo
bb8o$4boobooboo8bo$3b4oboobb8o$oobboobo3bo$9boob8o$11bo8bo$9bobb8o$9b
3o$8bo3b8o$3bo3b5o8bo$bb3obbo4b8o$bobboobobboo$boo4bobobb8o$4boobooboo
8bo19b73o$3b4oboobb8o$oobboobo3bo28b73o$9boob8o$11bo8bo19b73o$9bobb8o$
9b3o28b73o$8bo3b8o$3bo3b5o8bo19b35obob35o$bb3obbo4b8o52bobobobobo$bobb
oobobboo28b27obo15bob27o$boo4bobobb8o44bobobo15bobobo$4boobooboo8bo19b
19obo31bob19o$3b4oboobb8o36bobobo31bobobo$oobboobo3bo28b11obo47bob11o$
9boob8o28bobobo47bobobo$11bo8bo19b3obo63bob3o$9bobb8o20bobobo63bobobo!

A structured pattern for a Caterpillar

Structured patterns

Something I've been wanting to do for a while now is to produce a structured description of Gabriel Nivasch's Caterpillar.

In the context of the Game of Life, a "structured pattern" would be a description in terms of the smaller subpatterns that are repeated many times in the full pattern, such as the "shish-ke-babs" or the various rakes that make up the Caterpillar. The subpatterns in turn may be composed of smaller sub-subpatterns like pi climbers, blinkers, gliders, etc. A structured format makes a much better "blueprint" of a large pattern than a standard RLE encoding or picture-format file, and it's also very compact -- probably better compression than any standard binary-archive tool could manage.

Xlife 3.5/3.6 provides a good pattern format for describing this kind of structured pattern. Unfortunately it isn't quite versatile enough for this purpose. The big problem is that when you're dealing with periodic subpatterns, you often want to be able to include copies of them at several different phases. Xlife's approach is to define one phase of each periodic pattern as its "base" pattern; to paste multiple copies in, you paste the first base pattern, run the entire universe some number of generations to get the first pattern to the right phase relative to the second; then paste the second base pattern -- and if necessary run N more generations and paste a third base pattern, and so forth.

For stable patterns, or patterns that don't interact too closely, that's fine. But unfortunately this approach doesn't work very well for large numbers of subpatterns or higher periods -- sometimes Xlife's format doesn't support a "natural" compact definition based on subpatterns, because (for example) two of the subpatterns interfere with each other before the correct phase of the third subpattern can be placed to stabilize the whole conglomeration.

Ideas for an extension of Xlife #I format:

First, for reference, here is a summary of current Xlife syntax.

An extension of the format would fix the problem described above -- you'd have to be able to say, "run just this pattern in isolation for N generations, then paste it at (x,y)." This seems like a more natural way to compose patterns from subpatterns.

-- In fact, that's how Xlife's GUI does it! To register subpatterns in a "load script", you specify subpatterns' locations, transformations, and number of ticks forward in time from the base pattern. It's actually quite a surprise to look in an #I-format file for the first time and find out that Xlife has translated your registered subpatterns into this alternate format that is only sometimes equivalent.

I think Eugene Langvagen's PLife project has the necessary versatility to describe this kind of run-N-ticks-then-paste operation, but I haven't done enough benchmarking yet to know whether PLife can handle Caterpillar-sized structured patterns.

The main problem that I see is that a PLife script can easily become much too syntactically complex to be read directly by other Life software. You could create a structured pattern using a PLife script, but you'd have to convert it back to RLE to communicate it to anyone who doesn't have Python and PLife available. Xlife format is much more straightforward to write a parser for.

2c/3 transceiver, large size

The new 2c/3 receiver accepts diagonal signals from the track and uses a repeatable reaction to convert these signals into output gliders. (In the pattern as shown below, all the output gliders are blocked, but one or more of them could easily be allowed to escape by removing the appropriate eaters.)

This version of the receiver can process signals separated by 2175 or more generations. The incoming signal interacts with a small constellation of still lifes at the receiver end of the 2c/3 track (two blocks and an eater, shown in light green in the picture). With the assistance of a few catalysts, the constellation collapses cleanly into an R-pentomino, which is then guided onto a Herschel track.

The path of the active signal is shown in gray the image below; the direction of travel is indicated by the red arrows. Gliders from the output Herschel (short blue arrows) are used to create two more Herschels; the Herschels are then routed to various Herschel-to-glider converters, which produce five gliders in two salvos (long blue arrows). Four of these gliders collide to rebuild the original constellation. (The first glider just removes an extra block left by the conversion of the receiver's initial output R-pentomino to a Herschel.)

2c/3 signal receiver: Dave Greene, 6 February 2005

2c/3 details

2c/3 is a respectable speed in the Life universe; by comparison, a glider travels at only one-fourth of the speed of light, and it was proven many years ago that this is the fastest that any finite diagonal spaceship can travel through empty space. There is a similar limit of half of the speed of light for orthogonal spaceships.

However, disturbances in pre-existing structures can travel much faster than these limits -- there is no theoretical limit lower than lightspeed, either diagonally or orthogonally. See Gabriel Nivasch's lightspeed article for details and examples.

A signal in a 2c/3 track will quickly overtake a glider travelling in the same direction. If a sufficiently long track can be made to turn a corner, a 2c/3 signal in it will even overtake an orthogonal c/2 spaceship.

2c/3 transceiver, Mark Minus One

What follows is the first draft of a Game-of-Life circuit with a new, faster type of signal -- two-thirds of the speed of light diagonally! This is a big improvement in signal speed. Even Jason Summers' light-speed 'telegraph' can theoretically approach only half the speed of light diagonally, and it is considerably more unwieldy even than this pattern, and harder to re-use. Besides the telegraph, the fastest repeatable diagonal signal was a simple glider, at c/4.


Input is a Herschel, output is a glider. For comparison purposes, an extra reference glider has been added near the input Herschel. Despite the horrific and unnecessary inefficiency of the Herchel-to-2c/3 converter, and the fact that the output glider is produced from a 'backward' part of the 2c/3-to-glider converter, the output signal still manages to catch up to the reference glider!


Nothing about this pattern is properly optimized. For example, there's no good reason for the input Herschel ever to travel north; the conduit delivering the sacrificial beehive to the key point of the 2c/3 transmitter is ridiculously long; and the four boojum reflectors had to be moved embarrassingly far to the northwest to get the timings to work out.


The stair-step diagonal Herschel conduit at the left edge of the pattern is an artifact of an old toolkit I put together a year or two ago, which allows a shotgun for a synchronized glider salvo (like the three closely-spaced gliders traveling northeast from this area) to be constructed relatively quickly, though at considerable cost in efficiency. This part of the pattern took me less than an hour to put together, but it should be possible to fit a shotgun that fires twice as quickly into less than half the space.

After some optimization on the transmitter, it will be possible to use this technology to build the world's first period-independent pseudo-Heisenburp device, which can absorb a glider and produce as many output signals as needed -- including a new glider with exactly the same path and timing as the original!


[Previous Heisenburp devices all require the input glider to be aligned to some particular period, or they fail catastrophically. On the other hand, these periodic patterns can be "true" rather than "pseudo" Heisenburp devices: they produce output signals without destroying, or even temporarily affecting, the input glider.]


The 2c/3 signal track was discovered by Dean Hickerson in March 1997; Noam Elkies came up with several ingenious recipes for getting a repeatable signal started in a 2c/3 track, early this year, after I came up with a convoluted way of getting a signal out of a 2c/3 track. Further optimization is no doubt possible at both ends...

Update: May 1, 2007 -- Finally got around to doing the optimization work; the results can be seen in the latest version of the Golly project, Golly 1.2. Run heisenburp.py in the Scripts folder (you need to have Python installed, but it will take you all of maybe five minutes, and it's worth it.)

Glider-proof patterns

Copied from my postings to newsgroup: comp.theory.cell-automata
Date: 13 Feb 2005
Subject: Re: exist glider gun able of reconstruction in Life?


Ilmari Karonen wrote:

> This line of thought suggests another possibly interesting
>  question:  are there any known patterns that are fully
>  "glider-proof", in the sense that they can withstand a
>  collision with a single glider from any direction and in
>  any phase?

Among existing eater patterns in B3/S23 Life, I think the successful-defense record is still held by the eater2, which can absorb any number of gliders on any of four adjacent paths and emerge undamaged:

#Life 1.05
..*
*.*
.**
......*
....*.*
.....**
..........*
........*.*
.........**
..............*
............*.*
.............**
.
...............**.*
...............**.***
.....................*
...............**.***
................*.*
................*.*
.................*

-- For many stable patterns, by the way, there are other input glider lanes where the gliders are caught and turned into boats, which are then cleanly deleted by another glider coming in on the same lane. I'm not sure how to count those, though; if another glider then comes in on a different "glider-proof" lane, a boat would sometimes get in the way and cause an explosion.

So I suppose that's a different metric: any object will have a glider-pair-invulnerability percentage (!) higher or equal to the single-glider-invulnerability percentage. (Percentages could be calculated from the number of input glider lanes that allow a complete recovery, divided by the total number of input lanes that affect the object in any way.)

There's a double-sided version of the eater2 which I thought at first would have the highest known glider-invulnerability. By the above metric, if my quick counts are right, the double-sided eater2 is exactly 10% single-glider-proof, and 12.5% glider-pair-proof -- whereas the single-sided eater2 above is only 6% glider-proof -- 1/17 of the lanes are safe.

By comparison, a double-ended fishhook eater has a rating of 1/28 (3.6%) and a standard eater is down around 1/52 -- though the slow-glider-pair-proof ratings go up to 1/14 and 3/52, respectively...

However, it appears that one can string together double-sided eater2 patterns and increase the percentage rating indefinitely: each new eater2 added to the chain means that 18 more glider lanes will affect the object, of which 8 lanes are safe. So the glider-proof rating of these eater2 chains asymptotically approaches 4/9. Here's a 22% glider-proof eater2 chain, for example:

#Life 1.05
........................**
.........................*
....................**.*
....................**.**
.
....................**.**
...............**.*..*.**
...............**.**
.
...............**.**
................*.**
...........**.*
...........**.**
.
...........**.**
......**.*..*.**
......**.**
.
......**.**
.......*.**
..**.*
..**.**
.
..**.**
*..*.**
**

It takes one or two more eater2s to reach 25% (depending on whether glider-pair invulnerability is good enough) and further improvement gets slower and slower.

So it looks like maybe the first challenge would be to find something that breaks the 50% barrier. There might possibly be some clever way of getting those absorbing blocks one step closer together, but it doesn't look too likely to me...

-----------------------------

One more related topic:

Ilmari Karonen wrote:

>...  There are known CA's with indestructible patterns, but I'd be
>  surprised if Life had any.  However, the weaker condition of
>  "glider-proofness" doesn't intuitively seem quite as impossible
>  to me.

There's an even weaker form of the question which has the virtue of having a positive answer: it is technically possible to build an eater (of sorts) that can safely handle a wider "glider highway" than the eater2's four adjacent lanes. In fact, it can be shown that any given width of highway can be made single-glider-proof with a stable pattern -- or even multiple-glider-proof, as long as there's enough space between the gliders.

Last March I cobbled together a miscellaneous collection of stable Herschel conduits into a pattern that I called a "highway robber": it can absorb a glider coming in on one particular path -- let's call it "lane 0" -- and recover its initial configuration (very slowly!). It can also send out one or more output gliders to signal a capture from the highway. But in this case the important thing is that it allows gliders on adjacent lanes 1, 2, 3, ... of the highway to pass by
unharmed.

[Conventional small eaters based on boats or tub-with-tails (tubs-with-tail?) can almost manage this last trick --

#C 7x9 boat-based eater
.....*
......*
....***
.
.
**...*
*...*.*
.*...**
..*
*.*****
**....*
...***
**.*
*.*

-- they can absorb a glider on lane 0 and leave lanes 2, 3, 4 ... unaffected. As it happens, they also usually work on gliders coming in at 90 degrees from lane 0, that strike the eater at the same point. But they reliably blow up if a glider comes in on lane 1.]

A row of highway robbers watching adjacent lanes of a glider highway can absorb any slow glider salvo traveling along that highway. And setting several highway robbers to watch the same lane could reduce the minimum time between gliders by quite a bit.

But guarding a wide highway this way is hideously expensive -- the current highway-robber pattern is close to 400x400, though it could be made a good bit smaller. And it can only watch for gliders coming from one direction, of course -- if gliders can travel in both directions on the highway, you have to double the number of robbers so they can watch each others' backs.

Basically, every glider lane that you have to guard with this method just makes a pattern that much bigger and adds more unguarded lanes somewhere else. Figuring out how to build a complete glider-proof perimeter is very much an unsolved problem.

-------------------------------

So to return briefly to the original question: my instinct is that a stable pattern will never be 100% glider-proof -- there are too many possible lanes of attack -- and that even with an active pattern, it's going to be very hard to avoid having an Achilles' heel somewhere, at least during the detect-and-repair process. But it might at least be possible to design an active defense system with a reasonably high probability (above 99.99%, let's say) of recovering from a single random glider impact.

-- Just don't throw any orthogonal spaceships at it, or all bets are off!